Skip to main content

Preparation Manual

Print this page

Section 5: Sample Selected-Response Questions
Core Subjects EC–6 Subject Exam II—Mathematics (902)

Recommendation for individuals using a screenreader: please set your punctuation settings to "most."

This section presents some sample exam questions for you to review as part of your preparation for this Subject Exam. To demonstrate how each competency may be assessed, sample questions are accompanied by the competency that they measure. While studying, you may wish to read the competency before and after you consider each sample question. Please note that the competency statements do not appear on the actual exam.

For each sample exam question, there is a correct answer and a rationale for each answer option. The sample questions are included to illustrate the formats and types of questions you will see on the Subject Exam; however, your performance on the sample questions should not be viewed as a predictor of your performance on the actual exam.

Expand All Answers | Collapse All Answers

Subject Exam II Sample Questions

Competency 001—(Mathematics Instruction): The teacher understands how students learn mathematical skills and uses that knowledge to plan, organize and implement instruction and assess learning.

1. Students are working independently to solve the equation negative 4 plus question mark equals negative 10. The teacher says the following to help them understand the problem.

"If you owe somebody 4 dollars, you have a negative 4 dollar balance with that person. If you borrow more money from the person, you will owe more and have a more negative balance with that person."

After speaking with several students, the teacher finds that some of them are still having trouble with the concept of negative numbers. As a result, the teacher then reteaches the concept using a number line. Which of the following types of assessments has the teacher used?

  1. Formative
  2. Summative
  3. Formal
  4. Criterion
Answer. Enter to expand or collapse. Answer expanded
Option A is correct because formative assessment involves teachers' adjusting their instruction based on their assessment of students. The teacher in the scenario has conversations with the students and teaches again based on what is observed. Option B is incorrect because a summative assessment involves a teacher evaluating a student's learning, often at the end of a unit. It is usually a high-stakes test. Option C is incorrect because a formal assessment will give a teacher data. It is usually a test that has been used before, and data can be compared between students. Option D is incorrect because most criterion-referenced tests are used to simply tell if a student has learned the material, not to adjust instruction as described in the scenario.

2. A fifth-grade teacher writes the problem 56 times 12 on the board. Students begin to solve the problem mentally, and as each student finds a solution, he or she signals the teacher with a thumbs-up signal. When almost every student has given a thumbs-up signal, the teacher has the following dialogue with a student.

Teacher: "Billy, what answer did you come up with?"

Billy: "672."

Teacher: "Great job, Billy! That is the correct answer. Raise your hand if you found 672 to be the product, like Billy."

Almost every student in the class raised a hand. The teacher writes the next problem on the board.

Which of the following instructional adjustments can the teacher make to best assess all of the students' understanding of multiplying two-digit numbers?

  1. Allowing students to write their answers on paper, then collecting the papers at the end of the lesson
  2. Asking multiple students to share and defend their solutions before acknowledging the correct answer
  3. Asking students who did not hold up their thumbs to share their answer and explain
  4. Having Billy work the problem out on the board in front of the class
Answer. Enter to expand or collapse. Answer expanded
Option B is correct because the discussion gives the teacher an opportunity to hear how students are solving the problem. It will also give students an opportunity to share before they know their answer is wrong. Option A is incorrect because the students are only turning in their answers, not their work or their thinking. It will not show the teacher the level of their understanding. Option C is incorrect because it is only focusing on the students who did not raise their hand. More students may have missed the problem but were too shy to admit it. Option D is incorrect because the teacher is learning only about Billy's level of understanding, not that of the rest of the class.

3. Which of the following learning goals is most appropriate for a third-grade unit on money?

  1. Students will be able to determine the value of a collection of coins and bills.
  2. Students will be able to represent the value of a collection of coins as a fraction of a dollar.
  3. Students will be able to differentiate between money received as income and money received as gifts.
  4. Students will be able to solve problems involving money by performing operations on decimals to the hundredths place.
Answer. Enter to expand or collapse. Answer expanded
Option A is correct because this option correctly describes a Texas Essential Knowledge and Skill (TEK) for third grade math. A learning goal identifies what students will learn or be able to do as a result of instruction, not what they will be asked to do to demonstrate such learning. Options B, C and D are incorrect because they do not describe a learning goal that is appropriate for third grade.

4. Which of the following activities is most effective in helping kindergarten students understand measurement of the lengths of small objects, such as pencils or cups?

  1. Placing interlocking cubes next to the objects and counting the cubes.
  2. Cutting sheets of construction paper so that they are the same dimensions as the objects.
  3. Listening to the teacher explain how to line up a ruler next to the objects and mark their lengths.
  4. Watching the teacher demonstrate how to estimate the lengths of the objects using a child's hand or shoe.
Answer. Enter to expand or collapse. Answer expanded
Option A is correct because having the students count the number of interlocking cubes and placing the cubes next to each item provides a visual for the student to use in determining length. Option B is incorrect because cutting the construction paper would help in developing the concept of area and not length. Option C is incorrect because effectively measuring with a ruler involves concepts that have not been introduced yet in kindergarten. Option D is incorrect because using a hand or a shoe to estimate a length is more appropriate when the order of magnitude of the objects to measure is greater.

Competency 002—(Number Concepts and Operations): The teacher understands concepts related to numbers, operations and algorithms and the properties of numbers.

Word problem: Samantha' s Bakery sells cupcakes in packages of 12 and cookies in packages of 20. The bakery sold the same number of cupcakes and cookies yesterday. What is the minimum number of cupcakes that the bakery could have sold?

5. A teacher creates the word problem shown for a math lesson. Based on the word problem, the lesson will most likely cover which of the following mathematics concepts?

  1. Least common factor
  2. Greatest common factor
  3. Least common multiple
  4. Greatest common multiple
Answer. Enter to expand or collapse. Answer expanded
Option C is correct because finding the least common multiple will identify the smallest number of cupcakes sold. In fact, let x be the number of packages of cupcakes that were sold and y be the number of packages of cookies that were sold. The number of sold cupcakes will be 12x, and the number of sold cookies will be 20y. Clearly 12 divides 12x and 20 divides 20y. Since 12x equals 20y, 20 must also divide 12x. Since 12 and 20 both divide 12x, 12x is a common multiple of 12 and 20. The problem asks for the minimum (or least) number of cupcakes that could have been sold, so the least common multiple must be found to answer the question. Option A is incorrect because the least common factor is always 1. Option B is incorrect because the greatest common divisor is 4.
Option D is incorrect because there is no greatest common multiple.

6. Celeste is buying erasers for 8 of her friends. There are 76 erasers left at the store. Which of the following approaches can Celeste use to determine the greatest number of erasers she can buy to give each of her friends the same number and have none remaining?

  1. Drawing a picture of 76 erasers and circling groups of 8 before counting the number of groups created
  2. Creating a table in which one column represents the number of erasers at the store and the other represents the number of erasers each friend receives
  3. Using a standard algorithm learned previously in class to solve 76 divided by 8
  4. Making an organized list of the multiples of 8 to see which one is closest to 76
Answer. Enter to expand or collapse. Answer expanded
Option D is correct because the approach described provides the correct answer of how many erasers Celeste should buy at the store, 72. Options A, B and C are incorrect because the approaches described provide the number of erasers each friend will get, i.e., 7, not the total number of erasers Celeste should buy.

7. A first-grade teacher has set up the following math workstations for students to work in pairs.

Which of the following relationships are the students most likely exploring in the stations?

  1. Spatial concepts
  2. One more and one less
  3. Benchmarking numbers
  4. Part-part-whole
Answer. Enter to expand or collapse. Answer expanded
Option D is correct because in the activity, the students are conceptualizing that a number is made up of two or more parts. Option A is incorrect because in doing addition based on spatial relationships, students recognize the number of objects based on the way they are arranged. Option B is incorrect because in one-more-one-less relationships, students add and subtract 1 to a number.
Option C is incorrect because when students use benchmarks, they relate a number to 5 or 10.

Competency 003—(Patterns and Algebra): The teacher understands concepts related to patterns, relations, functions and algebraic reasoning.

Time 12:05 A.M. 2:05 A.M. 4:05 A.M. 5:05 A.M. 6:05 A.M.
Temperature 67 60 53 49.5 46

8. A cold front arrived at 12:05 A.M., and the subsequent temperatures were recorded in the table shown. If x represents the number of hours after 12:05 A.M., which of the following equations best represents the change in temperature as a function of time?

  1. y equals 3.5x plus 67
  2. y equals negative 7.1x plus 67
  3. y equals negative 7.1x minus 67
  4. y equals negative 3.5x plus 67
Answer. Enter to expand or collapse. Answer expanded
Option D is correct because the y-intercept represents the starting temperature, which was 67, and the slope represents the rate at which the temperature changed per hour, which was fraction 60 minus 67 over 2 minus 0 equals negative 3.5.
Options A and B are incorrect because the slope is incorrect. Option C is incorrect because both slope and y-intercept are incorrect.

Competency 004—(Geometry and Measurement): The teacher understands concepts and principles of geometry and measurement.

9. Which of the following geometric solids has five faces, eight edges and five vertices?

  1. A pentagonal pyramid
  2. A rectangular pyramid
  3. An octagonal prism
  4. A triangular prism
Answer. Enter to expand or collapse. Answer expanded
Option B is correct because a rectangular pyramid has one rectangular base and four triangular faces, eight edges and five vertices. Option A is incorrect because pentagons have five sides, so a pentagonal pyramid has six faces — one pentagonal base and five triangular faces. Option C is incorrect because an octagonal prism has ten faces — two octagonal faces and eight rectangular faces. Option D is incorrect because a triangular prism has five faces, nine edges and six vertices.

10. Which of the following statements best explains why the algebraic formula for the area of a triangle is 1 halfbh?

  1. A parallelogram can be transformed into a rectangle if a triangular piece is moved from one side to the other.
  2. The height of a triangle is not equal to the length of one of its sides, and the length must be divided by 2 to be used to find the area of the triangle.
  3. A parallelogram is composed of two congruent triangles, so the area of a parallelogram with the same base and height as the triangle can be divided by 2 to find the area of the triangle.
  4. This formula is only true for scalene triangles because all of their sides are different lengths, so one has to use the base and height to find the area.
Answer. Enter to expand or collapse. Answer expanded
Option C is correct because every parallelogram is made up of two congruent triangles. The formula for the area of a parallelogram is b times h, so the area of each of the two congruent triangles is half the area of the parallelogram. Two congruent triangles can always be arranged to form a parallelogram with the same base and the same height as the triangles. The area of the triangle will therefore be one-half as much as that of the parallelogram. Option A is incorrect because while the statement is true, it does not explain the formula for the area of a triangle. Option B is incorrect because it is logically faulty. Option D is incorrect because the area of every triangle can be found using the formula shown.

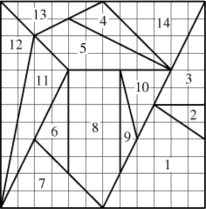
Archimedes' Stomachion puzzle

Diagram is a 12 by 12 grid that contains 12 different polygons. Only the figures in the answer choices will be described.
Figure 1 has a line that extends from the middle of the bottom border to the bottom corner of the right border. And another line that extends from the bottom right corner up 4 rows. From that point a diagonal line extends 2 rows up and 3 columns to the left. The last line extends from that point back to the middle of the bottom border.
Figure 3 has a line that begins 6 rows up and extends the last 3 columns to the right border. From that point a line extends all the way to the top corner of the right border. From that point a line extends diagonally from the top right corner 6 rows down and 3 columns to the left.
Figure 5 has a point that is 2 columns over from the left border and 10 rows up from the bottom. From that point a right diagonal line extends 2 columns and 2 rows down. From that point another line extends 6 columns to the right. From that point a left diagonal line extends 6 columns across and 3 rows up. The last line extends from that point to initial point of the figure.
Figure 8 has a diagonal line from the middle of the bottom border that extends 2 rows up and 2 columns to the left. From that point another line extends 6 rows up the same column. From that point a line extends across the row 3 columns to the right. From that point a line extends 6 rows down the same column. The last line extends from that point down 2 rows and over 1 column to left to the middle of the bottom border.
Figure 12 has a line that extends from the bottom of the left border all the way up to the top of the left border. From that point a line extends from the left top corner down 2 rows and across 2 columns on the right. From that point a line extends back down to the bottom left corner.

11. Archimedes' Stomachion puzzle from about 200 B.C. in which a 12-by-12 grid is divided into 12 different polygons, is shown above. A third-grade teacher is using the puzzle to determine whether or not students are able to partition or decompose nonstandard polygons to find their areas. Of which of the following polygons should the students be asked to find the area in order to demonstrate this skill?

Select all that apply.

  1. Figure 1
  2. Figure 3
  3. Figure 5
  4. Figure 8
  5. Figure 12
Answer. Enter to expand or collapse. Answer expanded
Options A, C and D are correct because Figure 1, Figure 5 and Figure 8 are nonstandard polygons, which are the focus of the lesson. Options B and E are incorrect because Figure 3 and Figure 12 are triangles.

Competency 005—(Probability and Statistics): The teacher understands concepts related to probability and statistics and their applications.

12. After learning the theoretical probability of a two-sided coin landing on any one side, students work in groups to flip the coin several times and get the following results: 9 heads and 6 tails. Based on the scenario, which of the following observations made by students about probability is accurate?

  1. The theoretical probability of a coin's landing on heads, 0.5, is equal to the experimental probability obtained.
  2. The theoretical probability of a coin's landing on heads is less than the experimental probability obtained.
  3. The experimental probability of a coin's landing on heads, 0.6, is lower than expected.
  4. The experimental probability would have been more accurate if the students had decreased the number of trials.
Answer. Enter to expand or collapse. Answer expanded
Option B is correct because the experimental probability and the theoretical probability of the coin's landing on heads are respectively 0.6 and 0.5. The theoretical probability is thus less than the experimental probability. Option A is incorrect because the experimental probability and the theoretical probability of the coin's landing on heads are not equal. Option C is incorrect because the experimental probability of the coin's landing on heads is greater than the theoretical probability. Option D is incorrect because as the number of trials (in this case a trial is flipping a coin) increases, the experimental probability gets closer to the theoretical probability.

Competency 006—(Mathematical Processes): The teacher understands mathematical processes and knows how to reason mathematically, solve mathematical problems and make mathematical connections within and outside of mathematics.

An equation is shown: 3 times the quantity 2 + 6 squared minus 4
new line: left bracket 3 left paren 2 right paren plus 3 left paren 6 right paren right bracket squared minus 4
new line: left paren 24 right paren squared minus 4
new line: 576 minus 4
last line: 572

13. A student simplifies the initial expression by applying the rule of order of operations. Which of the following best describes the student's error when simplifying the expression?

  1. The student added before evaluating the power of the exponents.
  2. The student evaluated the exponent before subtracting.
  3. The student multiplied before simplifying within grouping symbols.
  4. The student simplified the expression from left to right.
Answer. Enter to expand or collapse. Answer expanded
Option C is correct because the student multiplied before evaluating within the grouping symbol, violating the rule for order of operations: parentheses left to right, exponents left to right, multiplications or divisions left to right, additions or subtractions left to right. Option A is incorrect because the distributive property is not a rule in order of operations. Option B is incorrect because if the student had simplified the expression from left to right, the student would have gotten 3 times 2 equals 6; 6 plus 6 equals 12; 12 squared equals 144; 144 minus 4 equals 140. Option D is incorrect because the student was supposed to add before evaluating the power of the exponent, since addition fell within evaluating the expression in parentheses.

Word problem: A paint store is having a sale, and for every gallon of paint a customer purchases, the customer will receive one additional gallon for free. Write an equation for p, the number of gallons of paint received, in terms of x, the number of gallons of paint purchased.

14. A teacher asks students to solve the word problem shown. One student, John, says the answer is 2 plus x equals p. Which of the following activities will best help John recognize his misconception?

  1. Generating a model
  2. Creating a function table
  3. Using mental math
  4. Graphing the numbers
Answer. Enter to expand or collapse. Answer expanded
Option B is correct because a function table is a table of ordered pairs that follow a rule. The table will help the student identify the pattern. Option A is incorrect because generating a model is more appropriate for a geometric figure. Option C is incorrect because using mental math is less effective than teaching a student how to accurately use a strategy. Option D is incorrect because graphing the numbers is a skill that follows understanding and seeing the pattern and relating it to an expression.

Two scales appear.

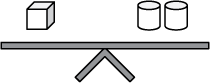
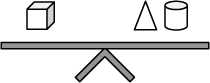
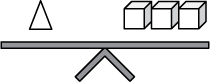
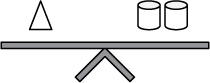
The scale on the left has one cube and one triangle on the left side of the scale and two cylinders on the right side of the scale. The scale of the right has one triangle on the left side of the scale and one cylinder and one cube on the right side of the scale.

15. In both figures shown, the scales are balanced. Which of the following scales is also balanced?

  1. Image of a scale with one cube on the left side and two cylinders on the right side.
  2. Image of a scale with one cube on the left side and one triangle and one cylinder on the right side.
  3. Image of a scale with one triangle on the left side and three cubes on the right side.
  4. Image of a scale with one triangle on the left side and two cylinders on the right side.
Answer. Enter to expand or collapse. Answer expanded
Option C is correct because of the following logic steps. Let's call the scale to the left scale 1 and the scale to the right scale 2.

Step 1: In scale 1 substitute a cylinder and a cube in place of the triangle, as per the equality in scale 2.
Step 2: Using the properties of equality, cancel a cylinder from both sides, obtaining a balanced scale, which will be called scale 3, with two cubes on a side and a cylinder on the other.
Step 3: In scale 2 substitute two cubes in place of the cylinder, as per equality in scale 3, obtaining a balanced scale with a triangle on one side and three cubes on the other. The latter balanced scale corresponds to the scale in Option C.

Option A is incorrect because one cylinder balances two cubes, as proved in step 2. If the scale in Option A were balanced, then substituting two cubes for each cylinder would give the scale a cube on one side and four cubes on the other. Option B is incorrect because replacing the triangle with a cylinder and a cube (scale 2) would give the scale a cube on one side and a cube and two cylinders on the other. Canceling a cube on each side would result in having two cylinders on one side and nothing on the other. Option D is incorrect because it would imply that a cube balances a cylinder. That is not true, as proved in step 2.

Return to Navigation