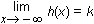Preparation Manual
Section 4: Sample Selected-Response Questions
TX PACT: Mathematics: Grades 4–8 (715)
Expand All Answers | Collapse All Answers
This section presents some sample exam questions for you to review as part of your preparation for the exam. To demonstrate how each competency may be assessed, sample questions are accompanied by the competency that they measure. While studying, you may wish to read the competency before and after you consider each sample question. Please note that the competency statements do not appear on the actual exam.
The correct answer is provided for each sample exam question. The sample questions are included to illustrate the formats and types of questions you will see on the exam; however, your performance on the sample questions should not be viewed as a predictor of your performance on the actual exam.
The following reference materials will be available to you during the exam:
Domain I—Number Sense and Operations
Competency 001—Understand numbers.
1. In the base-2 number system, the sum of 101 and 1011 is:
- 1000
- 1112
- 2000
- 10000
- Enter to expand or collapse answer.Answer expanded
- Option D is correct.
This question requires the examinee to analyze the role of place value in any number system. Align addends 101 and 1011 such that place values are in the appropriate columns. Add the two digits in the right column, 1 + 1 = 2. The 2 is regrouped as equaling 1 times 2 superscript 1 plus 0 times 2 superscript 0 with the 1 carried to the next column (Table 1). Continue the process until complete (Table 2), regrouping as needed, yielding the sum 10000.
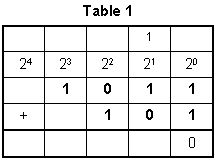
Table 1 blank blank blank 1 blank 2 superscript 4 2 superscript 3 2 superscript 2 2 superscript 1 2 superscript 0 blank 1 0 1 1 + blank 1 0 1 blank blank blank blank 0 
Table 2 1 1 1 1 blank 2 superscript 4 2 superscript 3 2 superscript 2 2 superscript 1 2 superscript 0 blank 1 0 1 1 + blank 1 0 1 1 0 0 0 0
Competency 002—Understand operations.
2. A car that is advertised for 28,900 dollars is sold after an 8% discount. If the commission rate is 0.75% of the sale price, how much money will the salesperson earn?
- $199.41
- $216.75
- $19,941.00
- $21,675.00
- Enter to expand or collapse answer.Answer expanded
- Option A is correct.
This question requires the examinee to solve a variety of problems involving ratios, proportions, and percents. The final sale price of the car is 92% of the asking price (100% minus 8% discount) and the salesperson earns 0.75% of the sale price. Commission = ($28,900)(0.92)(0.0075) = $199.41.
Domain II—Algebra and Functions
Competency 003—Understand patterns, relations, and functions.
3. A hiker climbs uphill at a steady pace, rests at a scenic spot for a while, then continues at a slower pace to the top of the hill. The hiker stops for lunch at the top, then decides to run down to the base of the hill. Which of the following graphs best expresses the hiker's speed as a function of time?
-
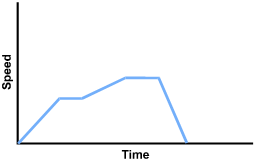
The first segment starts at the origin and slopes up to about a third the height of the vertical axis. The second segment is horizontal, for about half the horizontal distance of the first segment. The third segment slopes up less steeply than the first for about half the vertical distance of the first segment. The fourth segment is horizontal, and is a little longer than the previous horizontal segment. The fifth segment slopes steeply back to the horizontal axis.
-
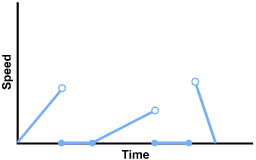
The first segment starts at the origin and slopes up to about a third the height of the vertical axis, ending with an open point. The second segment lies on the horizontal axis for about half the horizontal distance of the first segment, starting and ending with closed points. The third segment begins at the endpoint of the previous segment and slopes up less steeply than the first for about half the vertical distance of the first segment, ending with an open point. The fourth segment lies on the horizontal axis and is a little longer than the previous horizontal segment, starting and ending with closed points. The fifth segment starts with an open point at about the height of the endpoint of the first segment and slopes steeply back to the horizontal axis.
-
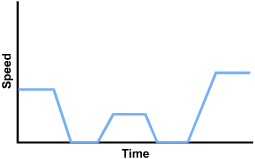
The first segment is horizontal, starting at about a third of the height of the vertical axis. It slopes steeply down to the horizontal axis for a horizontal segment a little shorter than the first horizontal segment. It slopes steeply to a third horizontal segment at about half the height of the first horizontal segment and a little shorter than the first. It slopes steeply down to another horizontal segment on the horizontal axis about the same length as the previous horizontal segment. It slopes steeply up to a horizontal segment about the same length as the first segment, at about half the height of the vertical axis.
-
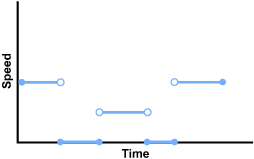
The first is at about 40% of the height of the vertical axis, starting with a closed point and ending with an open point. The second is on the horizontal axis, about the same length as the first, starting and ending with closed points. The third is about half the height of the first and a little longer, starting and ending with open points. The fourth is on the horizontal axis, shorter than the first, starting and ending with closed points. The fifth is at the same height as the first and about as long as the third, starting with an open point and ending with a closed point.
- Enter to expand or collapse answer.Answer expanded
- Option C is correct.
This question requires the examinee to analyze the properties of relations and functions in multiple representations (e.g., tables, graphs, equations, words). The "steady pace" held by the hiker reflects a constant speed over time; thus the first section of the graph is a horizontal line (slope equals zero) at some constant value of speed. The hiker slows to a resting position with a speed of zero, though time passes so the value for time continues to increase. The approach to the top of the hill shows a positive slope, with increasing speed and time as the hiker resumes walking, but since the pace is slower, the graph does not reach the previous level of speed. This pattern repeats when the hiker stops for lunch, but the run to the base reflects a greater speed than was achieved on the initial climb.
Competency 004—Understand algebraic techniques and applications.
4. If a person can buy up to 3 times as many desktop computers as laptop computers with the same amount of money, then which of the following inequalities relates the price of a desktop computer D to the price of a laptop computer L?
- D ≤ 3L
- D ≥ 3L
- 3D ≤ L
- 3D ≥ L
- Enter to expand or collapse answer.Answer expanded
- Option D is correct.
This question requires the examinee to connect appropriate algebraic notation to phrases and sentences. The condition of "up to 3 times as many" is the same as 1 laptop computer having the value of at most 3 desktop computers. Thus for the price of a desktop computer, D, and the price of a laptop computer, L, 3D ≥ L.
Competency 005—Understand linear relations and applications.
5. Which of the following is an equation of a line perpendicular to the line 4x - 9y = 12?
- y equals 9 fourths x plus 6
- y equals 4 ninths x plus 3
- y equals negative 4 ninths x minus 4
- y equals negative 9 fourths x minus 2
- Enter to expand or collapse answer.Answer expanded
- Option D is correct.
This question requires the examinee to analyze the relationship between a linear equation or inequality and its representations. The slope, m1, of the given line is found by isolating y in the given equation. 4x minus 9y equals 12 which becomes 9y equals 4x minus 12 which becomes y equals 4 ninths x minus 12 ninths and m1 equals 4 ninths. The slope, m perpendicular, of a line perpendicular to the given line is the negative reciprocal of the slope of the given line m1 . Thus m perpendicular equals negative 1 over m 1 so mperpendicular equals negative 9 fourths and y = negative 9 fourths x minus 2 must be the equation of the perpendicular line.
Competency 006—Understand nonlinear relations and concepts of calculus.
6. If the limit of function h of x equals a real number k as x goes to negative infinity, which of the following is the equation of an asymptote of the graph of h of x
- x = -k
- y = -k
- x = k
- y = k
- Enter to expand or collapse answer.Answer expanded
- Option D is correct.
This question requires the examinee to analyze function behavior in terms of limits, continuity, and rates of change. The situation described can be represented as the limit as x approaches negative infinity of h of x equals k. This means that as x approaches negative infinity, ? h of x approaches but never reaches k and that y = k is a horizontal asymptote.
Domain III—Measurement and Geometry
Competency 007—Understand measurement principles, procedures, and applications.
7. A car is traveling at a speed of 100 kilometers per hour. What is its approximate speed in meters per second?
- 28 meters per second
- 36 meters per second
- 280 meters per second
- 360 meters per second
- Enter to expand or collapse answer.Answer expanded
- Option A is correct.
This question requires the examinee to analyze the use of various units and unit conversions within the customary and metric systems. Both units in the given quantity must be converted: kilometers to meters and hours to seconds.
100 kilometers over 1 hour times 1000 meters over 1 kilometer times 1 hour over 3600 seconds equals 27.8 meters over second which approximately equals 28 meters over second.
Competency 008—Understand euclidean geometry in two and three dimensions.
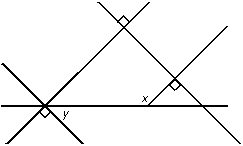 One is horizontal. Four other lines intersect the horizontal line at an unspecified angle that appears to be about 45 degrees. The first line passes through the horizontal line near the left side of the diagram, slanted from upper left to lower right, at point y. The second line passes through point y from lower left to upper right at a right angle to the first line. The third line intersects the second line at a right angle near the top of the diagram. The third line continues toward the lower right, passing through the horizontal line near the right side of the diagram. The fourth line starts at point x on the horizontal line and goes up toward the upper right corner of the diagram, passing through the third line at a right angle.
One is horizontal. Four other lines intersect the horizontal line at an unspecified angle that appears to be about 45 degrees. The first line passes through the horizontal line near the left side of the diagram, slanted from upper left to lower right, at point y. The second line passes through point y from lower left to upper right at a right angle to the first line. The third line intersects the second line at a right angle near the top of the diagram. The third line continues toward the lower right, passing through the horizontal line near the right side of the diagram. The fourth line starts at point x on the horizontal line and goes up toward the upper right corner of the diagram, passing through the third line at a right angle.
8. Five lines intersect as shown. If x and y are angle measures in degrees,
which of the following equations relates y to x in the diagram above?
- y equals 1 third x
- y = x - 90
- y equals 1 half x
- y = 180 - x
- Enter to expand or collapse answer.Answer expanded
- Option B is correct.
This question requires the examinee to analyze properties of points, lines, planes, and angles. If two lines are both perpendicular to the same transversal, the two lines are parallel. Thus there are two pairs of parallel lines in the figure. By the alternate interior angle theorem, x = y + 90° and y = x - 90°.
Competency 009—Understand coordinate and transformational geometry.
9. The end points of one diagonal of a parallelogram are (1, 3) and (1, -3). The end points of its other diagonal are (3, 1) and (-1, -1). What is the perimeter of the parallelogram?
-
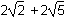
- 10
- 20
-
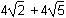
- Enter to expand or collapse answer.Answer expanded
- Option D is correct.
This question requires the examinee to connect algebra and geometry by applying concepts of distance, midpoint, and slope to classify figures and solve problems in the coordinate plane. Use points (1, 3) and (3, 1), then points (3, 1) and (1, -3), and the distance formula to find the length of two different sides of the parallelogram: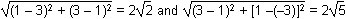 .
There are two of each of these sides, thus the perimeter of the parallelogram is
.
There are two of each of these sides, thus the perimeter of the parallelogram is
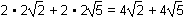 .
.
Domain IV—Statistics, Probability, and Discrete Mathamatics
Competency 010—Understand principles and techniques of statistics.
10. Which of the following types of data representation would be most useful for illustrating a correlation between two variables?
- a scatter plot
- a double bar graph
- a histogram
- a box-and-whisker plot
- Enter to expand or collapse answer.Answer expanded
- Option A is correct.
This question requires the examinee to use appropriate formats for organizing and displaying data. The scatter plot is the only one of the four choices that displays data that occur as ordered pairs for two variables.
Competency 011—Understand principles of probability and techniques for determining probability.
11. Milkshakes come in chocolate, vanilla, and strawberry flavors. Two people ordered milkshakes, but their orders were lost. If each person is given a randomly chosen flavor, what is the probability that they will both get the flavor that they ordered?
- 2/3 2 thirds
- 2/9 2 ninths
- 1/6 1 sixth
- 1/9 1 ninth
- Enter to expand or collapse answer.Answer expanded
- Option D is correct.
This question requires the examinee to determine probabilities of simple and compound events. The probability of one person getting the right flavor of shake is 1 third. The probability that the second person gets the right flavor is also 1 third. Since the two events are independent, the probability of the two people each getting the right flavor shake is 1 third times 1 third equal 1 ninth.
Competency 012—Understand principles of discrete mathematics.
12. Out of 600 businesses surveyed, 300 had Internet access, 450 had fax machines, and 50 had neither. How many of the businesses surveyed had both Internet access and fax machines?
- 100
- 150
- 200
- 250
- Enter to expand or collapse answer.Answer expanded
- Option C is correct.
This question requires the examinee to apply set theory to solve problems. Finding the number of businesses with both Internet access and fax machines means finding the number of elements in the intersection of the sets represented by I and F as defined below.
Let I = the number of businesses with just Internet access.
Let F = the number of businesses with just fax machines.
Let I intersection F equals the number of businesses with both Internet access and fax machines.
Equation 1: F plus I plus I intersection F equals 550 left parenthesis 600 minus the 50 with neither right parenthesis
Equation 2: I plus I intersection F equals 300
Equation 3: F plus I intersection F equals 450
Substituting I plus I intersection F from Equation 2 into Equation 1 gives F + 300 = 550, which implies F = 250.
Substituting this value for F in Equation 3 gives 250 plus I intersection F equals 450, which implies that I intersection F equals 200.