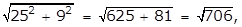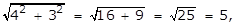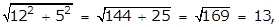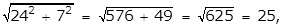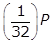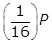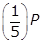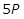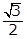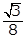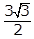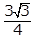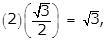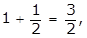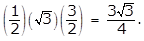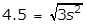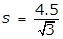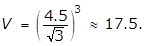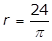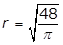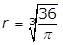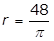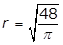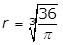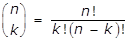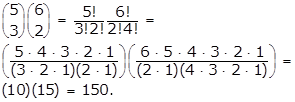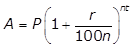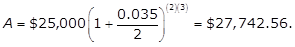Preparation Manual
Section 4: Sample Selected-Response Questions Mathematics 4–8 (115)
Expand All Answers | Collapse All Answers
Recommendation for individuals using a screenreader: please set your punctuation settings to "most."
This section presents some sample exam questions for you to review as part of your preparation for the exam. To demonstrate how each competency may be assessed, sample questions are accompanied by the competency that they measure. While studying, you may wish to read the competency before and after you consider each sample question. Please note that the competency statements do not appear on the actual exam.
For each sample exam question, there is a correct answer and a rationale for each answer option. The sample questions are included to illustrate the formats and types of questions you will see on the exam; however, your performance on the sample questions should not be viewed as a predictor of your performance on the actual exam.
The following reference materials will be available to you during the exam:
Domain I—Number Concepts
Competency 001—The teacher understands the structure of number systems, the development of a sense of quantity and the relationship between quantity and symbolic representations.
1. Which of the following right triangles has a hypotenuse with a length that is an irrational number?
- A right triangle with leg lengths of 4 and 3
- A right triangle with leg lengths of 12 and 5
- A right triangle with leg lengths of 24 and 7
- A right triangle with leg lengths of 25 and 9
- Enter to expand or collapse answer.Answer expanded
- Option D is correct because the length of the hypotenuse of a right triangle is given by the square root of the sum of the squares of the legs, and the square root of the quantity 25 squared plus 9 squared equals the square root of the quantity 625 plus 81 equals the square root of 706 which is an irrational number. Option A is incorrect because the square root of the quantity 4 squared plus 3 squared equals the square root of the quantity 16 plus 9 equals the square root of 25 equals 5 which is a rational number. Option B is incorrect because the square root of the quantity 12 squared plus 5 squared equals the square root of the quantity 144 plus 25 equals the square root of 169 equals 13 which is a rational number. Option C is incorrect because the square root of the quantity 24 squared plus 7 squared equals the squared root of the quantity 576 plus 49 equals the square root of 625 equals 25 which is a rational number.
Competency 002—The teacher understands number operations and computational algorithms.
2. Rectangle roman numeral 1 has dimensions a and b, and rectangle roman numeral 2 has dimensions a minus 2 and b + 2, where a is greater than 2 and b is greater than 0. Which of the following must be true?
- The area of rectangle roman numeral 1 is less than the area of rectangle roman numeral 2.
- The area of rectangle roman numeral 1 is greater than the area of rectangle roman numeral 2.
- The perimeter of rectangle roman numeral 1 is less than the perimeter of rectangle roman numeral 2.
- The perimeter of rectangle roman numeral 1 is equal to the perimeter of rectangle roman numeral 2.
- Enter to expand or collapse answer.Answer expanded
- Option D is correct because the perimeters of rectangles roman numeral 1 and roman numeral 2 are 2a + 2b and 2(a minus 2) + 2(b + 2) = 2a minus 4 + 2b + 4 = 2a = 2b, respectively, which are equal. Option A is incorrect because in the case a minus b is less than 2 the area of rectangle roman numeral 2 is (a minus 2)(b + 2) = ab + 2a minus 2b minus 4 = ab + 2(a minus b) minus 4, which is less than ab + (2)(2) minus 4 + ab, that is, less than the area of rectangle roman numeral 1. Option B is incorrect because in the case of a minus b is greater than 2, the area of rectangle roman numeral 2 is (a minus 2)(b + 2) = ab + 2a minus 2b minus 4 = ab + 2(a minus b) minus 4, which is greater than ab + (2)(2) minus 4 that is, greater than the area of rectangle roman numeral 1. Note that if a minus b = 2, then the area of rectangles roman numeral 1 and roman numeral 2 are equal. Option C is incorrect because it contradicts option D, which is true.
3. Which of the following is equivalent to the product (3 + 2i)(4 + 3i)?
- 6 + 17i
- 12 + 6i
- 18 + 17i
- 12 + 17i
- Enter to expand or collapse answer.Answer expanded
- Option A is correct because the product is 12 + 8i + 9i + 6i2 squared = 12 + 17i minus 6 = 6 + 17i. Option B is incorrect because the products of two binomials were not distributed properly during multiplication. Option C is incorrect because i2 squared is equivalent to negative 1, not 1. Option D is incorrect because the term 6i2 squared is neglected.
4. Which of the following is equivalent to 2 square root of 3 left paren square root of 2 plus square root of 3 right paren?
- 2 square root of 15
- 4 square root of 15
- 2 square root of 6 plus 6
- 18
- Enter to expand or collapse answer.Answer expanded
- Option C is correct because the expression can be simplified using the distributive property: 2 square root of 3 times square root of 2 plus square root of 3 = 2 square root of 3 left paren square root of 2 plus square root of 3 right paren equals left paren 2 square root of 3 right paren left paren square root of 2 right paren plus left paren 2 square root of 3 right paren left paren square root of 3 right paren equals 2 left paren square root of 3 right paren left paren square root of 2 right paren plus 2 left paren square root of 3 right paren left paren square root of 3 right paren equals 2 square root of 6 plus 2 square root of 9 equals 2 square root of 6 plus 2 left paren 3 right paren equals 2 square root of 6 plus 6. Option A is incorrect because the square root of 2 plus the square root of 3 does not equal the square root 5. Option B is incorrect because 2 square root of 6 plus 2 square root of 9 does not equal 4 square root of 15. Option D is incorrect because 2 left paren square root of 3 right paren left paren square root of 2 right paren plus 2 left paren square root of 3 right paren left paren square root of 3 right paren does not equal 2 left paren 6 right paren + 2 left paren 3 right paren equals 18.
Competency 003—The teacher understands ideas of number theory and uses numbers to model and solve problems within and outside of mathematics.
5. A traveler in Europe noticed on a certain day that 3.85 euros was worth 5.00 United States dollars. Based on this rate of exchange, 10 euros is approximately equal to how many United States dollars?
- 7.70
- 9.25
- 10.77
- 12.99
- Enter to expand or collapse answer.Answer expanded
- Option D is correct because the given numbers of dollars, d, and euros, e, can be related by the equation d = ke, where k equals 5 over 3.85 which approximately equals 1.299 is the rate of exchange in dollars per euro. Using the rate k when e = 10 yields d which approximately equals 12 dollars and 99 cents. Option A is incorrect because this response results from using an incorrect rate of exchange, 3.85 over 5 equals 0.77 euro per dollar, misapplied to 10 euros. Option B is incorrect because this response corresponds to multiplying d and e and then subtracting 10: left paren 5 right paren left paren 3.85 right paren minus 10. Option C is incorrect because this response corresponds to dividing e by d and then adding 10: 3.85 over 5 plus 10.
Domain II—Patterns and Algebra
Competency 004—The teacher understands and uses mathematical reasoning to identify, extend and analyze patterns and understands the relationships among variables, expressions, equations, inequalities, relations and functions.
6. An amount of 10 gallons of water is stored in a 15-gallon container. During the first 4 hours, the water evaporates from the container at a rate of 0.1 gallon per hour. During the next 5 hours, the water evaporates from the container at a rate of 0.3 gallon per hour. Which of the following functions represents the volume of water in the container, at time t, where 0 is less than or equal to t is less than or equal to 9?
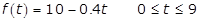 f of t equals ten minus point four t, where zero is less than or equal to t and t is less than or equal to nine
f of t equals ten minus point four t, where zero is less than or equal to t and t is less than or equal to nine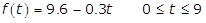 f of t equals nine point six minus point three t, where zero is less than or equal to t and t is less than or equal to nine
f of t equals nine point six minus point three t, where zero is less than or equal to t and t is less than or equal to nine f of t equals left brace case one first line ten minus point one t, where zero is less than or equal to t and t is less than or equal to four;
case two second line nine point six minus point three t, where 4 is less than t and t is less than or equal to nine
f of t equals left brace case one first line ten minus point one t, where zero is less than or equal to t and t is less than or equal to four;
case two second line nine point six minus point three t, where 4 is less than t and t is less than or equal to nine f of t equals left brace case one first line fifteen minus point one t, where zero is less than or equal to t and t is less than or equal to four;
case two second line ten minus point four t, where 4 is less than t and t is less than or equal to nine
f of t equals left brace case one first line fifteen minus point one t, where zero is less than or equal to t and t is less than or equal to four;
case two second line ten minus point four t, where 4 is less than t and t is less than or equal to nine
- Enter to expand or collapse answer.Answer expanded
- Option C is correct because water evaporates at a rate of 0.1 gallon per hour during the first 4 hours. After 4 hours, there are 10 minus left paren 0.1 right paren left paren 4 right paren equals 9.6 gallons left. For the next 5 hours, the rate of evaporation is 0.3 gallon per hour. Option A is incorrect because the rate of evaporation is not a constant 0.4 gallon per hour. Option B is incorrect because the initial amount is 10 gallons of water, and the rate of evaporation is not a constant 0.3 gallon per hour. Option D is incorrect for several reasons. For example, the initial amount is 10 gallons of water, not 15.
7. Each week last year, a small manufacturer earned a profit by selling handbags. The weekly profit P from selling x handbags is modeled by the function P of x = negative 0.5x squared plus 40x minus 300. Based on the model, what was the maximum weekly profit, in dollars, that the manufacturer could have earned last year?
- 300 dollars
- 450 dollars
- 500 dollars
- 700 dollars
- Enter to expand or collapse answer.Answer expanded
- Option C is correct because the given function is quadratic, and therefore, its graph is a parabola that opens downward. The maximum possible weekly profit is the value of the function at the vertex of the parabola. The x-coordinate of the vertex can be found using the formula x equals negative fraction b over 2a equals negative fraction 40 over 2 left paren negative 0.5 right paren equals 40, where a and b are the coefficients of the x squared term and the x term, respectively. Substituting x equals 40 in the function gives the value P of 40 equals 500 at the vertex. Therefore, the maximum possible profit is 500 dollars. Option A is incorrect because it corresponds to an x-coordinate of x equals b over 2 equals 40 over 2 equals 20 at the vertex, whereby the value would be P of 20 equals 300. Option B is incorrect because it corresponds to an x-coordinate of x equals 30 at the vertex, whereby the value would be P of 30 equals 450. Option D is incorrect because it corresponds to an x‑coordinate of x equals 20 at the vertex and a subsequent computation of the value using the incorrect function P of x equals 0.5x squared plus 40x minus 300, whereby the value would be P of 20 equals 700.
8. Ms. Johnston is a sales associate at a jewelry store. Her total weekly earnings consist of a wage of $10 per hour plus a 10 percent commission on her total sales for the week. One week Ms. Johnston worked 30 hours and had total sales of x dollars. Which of the following represents her total weekly earnings y, in dollars, for that week?
- y equals 10x plus 0.01
- y equals 0.1x plus 300
- y equals 0.1 left paren x plus 300 right paren
- y equals 30 left paren 0.1x plus 10 right paren
- Enter to expand or collapse answer.Answer expanded
- Option B is correct. Ms. Johnston's total earnings are 10 dollars times the number of hours worked, plus 10% of her total sales: y equals 10 left paren 30 right paren plus 10 over 100 x equals 0.1x plus 300. Option A is incorrect because x represents the total sales, not the number of hours worked. Option C is incorrect because this equation results from applying the 10% commission after adding the value of sales and the 300 dollars base earnings. Option D is incorrect because this equation results from multiplying the 30 hours by the 10 dollars -per-hour base pay rate and the 10% commission.
Competency 005—The teacher understands and uses linear functions to model and solve problems.
9. Which of the following is the equation of the line in the xy-plane that passes through the points (negative 7, negative 2) and (negative 2, negative 7)?
- x + y = negative 9
- x minus y = negative 9
- x minus y = negative 5
- negative x + y = negative 5
- Enter to expand or collapse answer.Answer expanded
- Option A is correct because the values (x, y) of both of the ordered pairs satisfy the equation; that is, the graph of the equation passes through the points in the xy-plane. Option B is incorrect because neither of the ordered pairs satisfies the equation; that is, the graph of the equation does not pass through either point in the xy-plane. Option C is incorrect because the values (negative 2, negative 7) do not satisfy the equation; that is, the graph of the equation does not pass through that point in the xy-plane. Option D is incorrect because the values (negative 7, negative 2) do not satisfy the equation; that is, the graph of the equation does not pass through that point in the xy-plane.
10. In the xy-plane, line segment AB is bisected by line segment CD, and the coordinates of the point of intersection are (negative 2, negative 3). If the coordinates of A are (negative 8, negative 1), what are the coordinates of point B ?
- (5, negative 5)
- (4, negative 5)
- (negative 5, negative 2)
- (8, 1)
- Enter to expand or collapse answer.Answer expanded
- Option B is correct because (negative 2, negative 3) is the midpoint of segment AB, meaning that point B must lie on the line that connects the two points (negative 2, negative 3) and (negative 8, negative 1), and the distance from B to (negative 2, negative 3) is the same as the distance from A to (negative 2, negative 3). The line y = negative 1 third x minus 11 over 3 is the line that contains A and (negative 2, negative 3), and thus also contains B. The distance between the point A and (negative 2, negative 3) is 2 square root 10. The equation of the set of points that lies at a distance of 2 square root 10 from (negative 2, negative 3) is the quantity of x plus 2 squared plus the quantity of y plus 3 squared equals 40. Solving the system of equations, y = negative 1 third x minus 11 over 3 and the quantity of x plus 2 squared plus the quantity of y plus 3 squared equals 40, produces the solutions (4, negative 5) and (negative 8, negative 1). Options A, C and D are incorrect because they do not lie at the same distance from (negative 2, negative 3) as (negative 8, negative 1).
11. A restaurant charges 9 dollars for a large pizza and 1 dollar and 75 cents for each topping selected. Let C be the total cost of a pizza and let t be the number of toppings selected. Which of the following is an equation for the total cost C of a pizza?
- C equals 9.00 + 1.75t
- C equals (1.75 + 9.00)t
- C equals 9.00t + 1.75
- C equals left paren 1.75 right paren left paren 9.00 right paren t
- Enter to expand or collapse answer.Answer expanded
- Option A is correct because if a customer orders t toppings, the total charge will be 1 dollar and 75 cents t plus the base cost of 9 dollars. Option B is incorrect because the multiplier of t should only be used with the cost of each topping. Option C is incorrect because 9 dollars is the base cost of the pizza; it should not be multiplied by the number of toppings ordered. Option D is incorrect because the individual costs should be added, not multiplied.
Competency 006—The teacher understands and uses nonlinear functions and relations to model and solve problems.
12. Which of the following points is the vertex of the graph of y equals 2x squared minus 8x plus 1 in the xy-plane?
- (2,13)
- (0,1)
- (4,1)
- (2,negative 7)
- Enter to expand or collapse answer.Answer expanded
- Option D is correct because the vertex form of a parabola is y equals a left paren x minus h right paren squared plus k where the coordinates of the vertex are (h, k). The equation can be rewritten as y equals 2 left paren x minus 2 right paren squared minus 7; therefore, the vertex of the graph is the point (2,negative 7). Options A, B and C are incorrect because they result from mistakes in calculation of the vertex form of the equation.
13. Which of the following values of x satisfies 2x squared plus 5x minus 3 is less than 0?
- negative 3
- 1 third
- 1 half
- 2
- Enter to expand or collapse answer.Answer expanded
- Option B is correct. The function f of x = 2xsquared plus 5x minus 3 is equal to zero when x = negative 3 or x = 1 half. The value of f is less than zero for all x such that negative 3 is lesss than x is less than 1 half. Of the options listed, only 1 third is greater than negative 3 and less than 1 half. Options A and C are incorrect because f of x equals 0 when x equals negative 3 or x equals 1 half. Option D is incorrect because f of x is greater than 0 when x equals 2.
14. An eighth-grade mathematics teacher is preparing a lesson about exponential decay and plans to use an example involving half-life. The teacher explains that half-life is the amount of time required for the initial quantity of a substance to reduce by half, and the teacher then gives an example of a radioactive substance with a half-life of 40 years. If the initial quantity of the radioactive substance is P grams, what is the quantity, in grams, that will remain after 200 years?
- Enter to expand or collapse answer.Answer expanded
- Option A is correct because if the initial quantity is P grams,
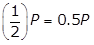 will remain after 40 years. In 200 years there are
will remain after 40 years. In 200 years there are 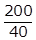 , or five, 40-year periods. The quantity remaining after five 40-year periods will be
, or five, 40-year periods. The quantity remaining after five 40-year periods will be 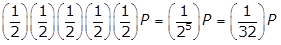 left paren one half right paren left paren one half right paren left paren one half right paren left paren one half right paren left paren one half right paren P equals left paren one over 2 to the fifth power right paren P equals left paren one thirty second right paren P grams. Option B is incorrect because the quantity
left paren one half right paren left paren one half right paren left paren one half right paren left paren one half right paren left paren one half right paren P equals left paren one over 2 to the fifth power right paren P equals left paren one thirty second right paren P grams. Option B is incorrect because the quantity 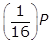 grams is what will remain after only four half-life periods. Option C is incorrect because
grams is what will remain after only four half-life periods. Option C is incorrect because 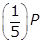 is
is 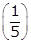 of the original amount. Option D is incorrect because the quantity of the substance will decrease as it decays exponentially, not increase.
of the original amount. Option D is incorrect because the quantity of the substance will decrease as it decays exponentially, not increase.
Competency 007—The teacher uses and understands the conceptual foundations of calculus related to topics in middle school mathematics.
Use the figure below to answer the question that follows.
The left vertex of the base is at 1 on the x axis, and the right vertex of the base is at 4 on the x axis. The sides are vertical. A data line marked as y equals 1 third x plus 3 extends from the left of the y axis to the right edge of the plot space. A portion of this line forms the top edge of the trapezoid.
15. A geometry teacher developed a lesson that incorporates solving linear equations using algebra and finding the area of geometric shapes using geometry. Which of the following calculus topics could be demonstrated by finding the area of the trapezoid above?
- The derivative of a function at a point
- The definite integral
- The limit of a function of x as x goes to infinity
- Newton's method to find the zeros of a function
- Enter to expand or collapse answer.Answer expanded
- Option B is correct because the definite integral is the area of the region in the xy-plane between the x-axis and the graph of a function over a given interval, where the region in this case is a trapezoid. Option A is incorrect because the derivative of a function at a point is the instantaneous rate of change of the function at the given point. Option C is incorrect because the limit of a function as x goes to infinity, if it exists, is a value L that the functional values of f of x are arbitrarily close to as x is arbitrarily large. Option D is incorrect because Newton's method is used to find a zero of a function and not the area.
Domain III—Geometry and Measurement
Competency 008—The teacher understands measurement as a process.
Use the figure below to answer the question that follows.
Each has a horizontal line extending to the right of its base, representing the length of the object's shadow, and an angled line from the right end of the shadow to the top of the object. The yardstick is dimensioned as 3 feet high with a shadow 5 feet long. The tree's shadow is dimensioned as 26 feet long. There is a note that says Figure not to scale.
16. At a certain time of day, a student measured the height of the shadow of a yardstick, held vertically, to be 5 feet. At the same time of day, the student measured the length of the shadow of the tree to be 26 feet. To the nearest foot, what is the height of the tree?
- 16 feet
- 24 feet
- 30 feet
- 43 feet
- Enter to expand or collapse answer.Answer expanded
- Option A is correct because a line drawn from the top of the yardstick to the end of the shadow forms the same angle as a line drawn from the top of the tree to the end of its shadow. Therefore, these two triangles are similar by angle-angle-angle similarity. One of the proportions that follows from similarity is 3 over 5 equals h over 26, where h is the height of the tree. Solving for h yields h = 15.6, which, rounded to the nearest foot, is approximately 16 feet. Option B is incorrect because it is erroneously obtained from 26 minus 5 equals 21 and 21 plus 3 equals 24. Option C is incorrect because it results from finding the hypotenuse of the larger triangle:
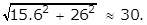 Option D is incorrect because it results from the incorrect proportion 3 over 5 equals 26 over h.
Option D is incorrect because it results from the incorrect proportion 3 over 5 equals 26 over h.
17. Frank completed a 400-meter race in 75 seconds. Which of the following is closest to Frank's speed in kilometers per hour?
- 17 kilometers per hour
- 19 kilometers per hour
- 21 kilometers per hour
- 23 kilometers per hour
- Enter to expand or collapse answer.Answer expanded
- Option B is correct because 400 meters over 75 seconds times 3600 seconds over 1 hour times 1 kilometer over 1000 meters equals 19.2 kilometers. Among the options presented, 19 kilometers per hour is the closest to the exact value. Options A, C, and D are incorrect because 19 kilometers per hour is closest to the actual value of 19.2 kilometers per hour.
18. Tony purchased 100 kilograms of decorative stones. Each stone weighs approximately 10 grams. Which of the following is the best estimate of the number of stones purchased?
- 10 cubed
- 10 to the power of 4
- 10 to the power of 5
- 10 to the power of 6
- Enter to expand or collapse answer.Answer expanded
- Option B is correct because there are 1000 grams in a kilogram, so 100 times 1000 equals 10 squared times 10 cubed equals 10 to the power of 2 plus 3 equals 10 to the power of 5 grams of stones were purchased. Since each stone weighs approximately 10 grams, about 10 to the power of 5 over 10 to the power of 1 equals 10 to the power of 5 minus 1 equals 10 to the power of 4 stones were purchased. Option A is incorrect because 10 cubed equals 1000 is the number of grams in a kilogram. Option C is incorrect because 10 to the power of 5 equal 100,000 is the total number of grams of stones purchased. Option D is incorrect because 10 to the power of 6 equals 1,000,000 is the total number of grams of stones purchased times the weight per stone.
Competency 009—The teacher understands the geometric relationships and axiomatic structure of Euclidean geometry.
Use the figure below to answer the question that follows.
A diagonal line from upper left to lower right passes through both of the horizontal lines. At the intersection of the diagonal line with l sub 1, the angles are labeled, clockwise from upper left, a, b, c, and d. At the intersection of the diagonal line with l sub 2, the angles are labeled, clockwise from upper left, e, f, g, and g.
19. In the diagram above, l sub 1 is parallel to l sub 2. If the measure of angle b is 100 degrees, what is the measure of angle e?
- 100 degrees
- 95 degrees
- 80 degrees
- 75 degrees
- Enter to expand or collapse answer.Answer expanded
- Option C is correct. Based on the figure, angles a and b are supplementary, so the sum of their measures is 180 degrees. Since the measure of angle b is 100 degrees, the measure of angle a is 80 degrees. Because l sub 1 and l sub 2 are parallel lines cut by a transversal, corresponding angles are congruent and the measures are equal. Therefore, the measure of angle a is equal to the measure of angle e, and the measure of angle e is thus also 80 degrees. Options A, B and D are incorrect because the measure of angle e is 80 degrees.
Use the figure below to answer the question that follows.
Above line l is a point labeled P. A vertical line passes through point P and the horizontal line. Two short arc segments pass through line l on either side of the vertical line. They are equidistant from the vertical line and appear to be segments of a circle with P as their center point. Two other short arc segments pass through the vertical line, intersecting each other below line l. They appear to have been drawn with their center points at the intersections of the first arcs and the horizontal line.
20. Which of the following describes the geometric construction above, where the construction uses only a compass and a straightedge?
- The locus of points that are equidistant from line l and point P
- The line perpendicular to line l and passing through point P
- The extension of line l
- The line parallel to line l and passing through point P
- Enter to expand or collapse answer.Answer expanded
- Option B is correct because the arcs that intersect line l at two points, call them A and B, appear to be part of a circle centered at point P, and the two other arcs that intersect each other at a point (call it C) appear to be from two circles centered at A and B with equal radii. If A, B, and C are constructed with a compass as they appear to be, then PA = PB and CA = CB. The line passing through points P and C is then drawn with a straightedge, intersecting l at a point (call it D) and the two equalities yield two congruent triangles, APC and BPC. From this congruence, it follows that triangles APD and BPD are congruent. Finally, it follows that the four angles at D are right angles, and line PC is a line that is perpendicular to l and passes through P. Option A is incorrect because the locus of points equidistant from a line and a point that is not on the line is a parabola, which does not appear in the figure. Option C is incorrect because line l is given. Option D is incorrect because there are no parallel lines in the figure.
21. Let ABC be a triangle, where AB has length 4 and BC has length 8. For which of the following possible lengths of AC is ABC an obtuse triangle?
Select all that apply.
- 6
- 7
- 8
- 9
- 10
- Enter to expand or collapse answer.Answer expanded
- Options A, D and E are correct because a triangle has an obtuse angle if, and only if, the square of the longest length is greater than the sum of the squares of the two shorter lengths. This is true because when "greater than" is replaced by "equal to," the triangle is a right triangle, using the Pythagorean theorem. The inequalities for options A, D and E are 8 squared is greater than 4 squared plus 6 squared, 9 squared is greater than 4 squared plus 8 squared, and 10 squared is greater than 4 squared plus 8 squared, respectively. Option B is incorrect because 8 squared is less than 4 squared plus 7 squared. Option C is incorrect because 8 squared is less than 4 squared plus 8 squared.
Competency 010—The teacher analyzes the properties of two- and three-dimensional figures.
Use the figure below to answer the question that follows.
There is a figure of an equilateral triangle inside a circle such that each vertex of the triangle lies on the circumference of the circle. The vertices of the triangle are labeled A, B, and C, with line A C forming the base. A vertical line is drawn from the apex of the triangle at point B to point D on the baseline A C. The vertical line is marked as being perpendicular to line A C. The angle at point A is dimensioned as 60°. A radial line, dimensioned as 1, is drawn from the center of the circle at point O to point C. The radial line forms the hypotenuse of a triangle ODC with line DC as the base and line D O as the vertical leg. Angle OCD is dimensioned as 30°, and angle D O C is dimensioned as 60°.
22. Equilateral triangle ABC is inscribed in a circle with center O and a radius of 1, as shown above. The height of the triangle is BD. What is the area of triangle ABC?
- the square root of 3 over 2
- the square root of 3 over 8
- 3 the square root of 3 over 2
- 3 the square root of 3 over 4
- Enter to expand or collapse answer.Answer expanded
- Option D is correct because the area of a triangle is 1 halfbh, where b is the base and h is the height. In the triangle shown, AC is the base and BD is the height. Since triangle ABC is an equilateral triangle, angles A, B and C all have measures of 60 degrees. The radius OC bisects angle BCA, so the measure of angle OCD is 30 degrees. Thus, triangle OCD is a 30-60-90 triangle, and the length of OC is 1 because OC is a radius of the circle centered at O. Therefore, the length of OD is 1 half and the length of DC is square root of 3 over 2. Thus, the length of AC, the base of the triangle, is left paren 2 right paren left paren square root of 3 over 2 right paren equals square root of 3 the length of BD, the height, is 1 plus 1 half equals 3 over 2 and the area is left paren 1 half right paren left paren square root of 3 right paren left paren 3 over 2 right paren equals 3 square root of 3 over 4 Options A, B and C are incorrect because they are not areas of the triangle ABC.
Use the cube below to answer the question that follows.
There is a line drawing of a cube with invisible sides so that all of the edges are visible. A dashed line is drawn from the far upper left corner to the near lower right corner, passing through the center of the cube.
23. In the cube shown above, a student measured the length of a diagonal to be 4.5 centimeters. Which of the following is the best estimate of the volume of the cube?
- 121.5 cubic centimeters
- 91.1 cubic centimeters
- 17.5 cubic centimeters
- 2.6 cubic centimeters
- Enter to expand or collapse answer.Answer expanded
- Option C is correct because the volume V of a cube with edges of length s is s cubed. The diagonal has length 4.5 equals square root of 3 s squared, and thus, s equals 4.5 over square root of 3. Therefore, V equals left paren 4.5 over square root 3 right paren cubed is approximately equal to 17.5 Option A is incorrect because it is the surface area of the cube, where 4.5 is the length of an edge. Option B is incorrect because it is approximately the volume of the cube, where the length of an edge is 4.5. Option D is incorrect because it is approximately the length of an edge of the cube.
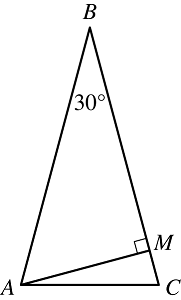
The shortest side, A C, is horizontal. Angle A B C is dimensioned as 30°. A line is drawn from vertex A to point M on side B C, forming a right angle with side B C.
24. In triangle ABC shown, AB = BC, the measure of angle ABC is 30 degrees, and line segment AM is perpendicular to side BC. What is the degree measure of angle MAC?
- 10 degrees
- 15 degrees
- 60 degrees
- 75 degrees
- Enter to expand or collapse answer.Answer expanded
- Option B is correct. Since AB = BC, the triangle shown, ABC, is isosceles, and therefore the measure of angle BAC must be equal to the measure of angle BCA. The sum of the measures of angles ABC, BAC, and BCA must be 180 degrees. Let x be the measure of angle BAC; then x is also the measure of angle BCA, and 30 degrees plus 2x degrees equals 180 degrees. Thus, x equals 180 minus 30 over 2 equals 75 degrees. Triangle AMB is a right triangle, so the measure of angle BAM is 90 degrees minus 30 degrees equal 60 degrees. The measure of angle BAC is the sum of the measures of angles BAM and MAC, so the measure of angle MAC is 75 degrees minus 60 degrees equal 15 degrees. Options A, C, and D are incorrect because the measure of the angle is 15 degrees.
25. A circle with radius r has a circumference of 48. What is the value of r?
- r equals 24 over pi
- r equals the square root of 48 over pi
- r equals cube root of 36 over pi
- r = 48 over pi
- Enter to expand or collapse answer.Answer expanded
- Option A is correct. The circumference C of a circle of radius r is C = 2πrC equals 2 pi r. It is given that C = 48, therefore 2πr = 482 pi r = 48 and r equals 48 over 2 pi equals 24 over pi. Option B is incorrect because r equals square root 48 over pi is obtained by incorrectly using the formula for the area of a circle, pi r squared equals 48. Option C is incorrect because r equals cube root of 36 over pi is obtained by incorrectly using the formula for the volume of a sphere, 4 over 3 pi r cubed equals 48. Option D is incorrect because r equals 48 over pi is obtained by incorrectly using r for the diameter of the circle instead of the radius, pi r equals 48.
Competency 011—The teacher understands transformational geometry and relates algebra to geometry and trigonometry using the Cartesian coordinate system.
Use the figure below to answer the question that follows.
The coordinates of point A are 2, 8. The coordinates of point B are 14, 8. The coordinates of point C are 14, 3
26. Triangle A′B′C′ has a hypotenuse of length 52 and is a dilation of triangle ABC shown above. What is the scale factor used to dilate triangle ABC to transform it to triangle A′B′C′?
- 1 over 4
- 4 over 13
- 13 over 4
- 4
- Enter to expand or collapse answer.Answer expanded
- Option D is correct because, using the Pythagorean theorem, the hypotenuse of triangle ABC is 13, and since the hypotenuse of A′B′C′ is 52, it follows that triangle ABC has been dilated by a factor of 52 over 13, or 4. Option A is incorrect because it is equal to the reciprocal of 52 over 13. Option B is incorrect because it assumes that the hypotenuse of triangle ABC is 132 squared, or 169, in which case the dilation factor would be 52 over 169, or 4 over 13. Option C is incorrect because it assumes that the hypotenuse of triangle ABC is 132 squared, or 169, and then uses the reciprocal of what would be the dilation factor, that is, the reciprocal of 52 over 169, or 13 over 4.
Domain IV—Probability and Statistics
Competency 012—The teacher understands how to use graphical and numerical techniques to explore data, characterize patterns and describe departures from patterns.
Use the list below to answer the question that follows.
90, 70, 60, 75, 80, 82, 85, 88, 80, x
27. The list above shows ten scores from a recent test in a math class. The range of the ten scores is 30, and the interquartile range is 10. Which of the following could be the value of x ?
- 74
- 84
- 86
- 96
- Enter to expand or collapse answer.Answer expanded
- Option B is correct. The range of the numbers in a data set is the difference between the greatest number and the least number in the data set. The quartiles are obtained by ordering the data from the least value to the greatest value and then dividing the data into four equal groups. The interquartile range is the difference between the third quartile and the first quartile. Using the value of 84 from option B and ordering the list from least to greatest—60, 70, 75, 80, 80, 82, 84, 85, 88, 90—the range is 90 minus 60 equals 30, the first quartile is 75, the third quartile is 85, and the interquartile range is 85 minus 75 equals 10. Option A is incorrect because using the value of 74 from option A and ordering the list from least to greatest—60, 70, 74, 75, 80, 80, 82, 85, 88, 90—the range is the first quartile is 74, and the third quartile is 85, so the interquartile range is 85 minus 74 equals 11. Option C is incorrect because using the value of 86 from option C and ordering the list from least to greatest—60, 70, 75, 80, 80, 82, 84, 85, 86, 88, 90—the range is 90 minus 60 equals 30, the first quartile is 75, and the third quartile is 86, so the interquartile range is 86 minus 75 equals 11. Option D is incorrect because using the value of 96 from option D and ordering the list from least to greatest—60, 70, 75, 80, 80, 82, 85, 88, 90, 96—the range is 96 minus 60 equals 36.
Use the circle graph below to answer the question that follows.
From the top, in a clockwise direction, the wedges are labeled Red, Green, Blue, and Yellow. The red wedge occupies nearly all of the right half of the circle. The green wedge is about an eighth of the circle. The blue wedge is about a quarter of the circle. The yellow wedge is about a sixth of the circle.
28. Ms. Jefferson read an article to her class describing a survey of students who were asked to choose their favorite color among the colors yellow, blue, green, and red. The graph above shows the results of the survey. Ms. Jefferson tells the class that the survey results are representative of all students, and she asks the class to predict how many of the 850 students in their school would choose either yellow or green. Which of the following is the best estimate?
- 20
- 25
- 150
- 250
- Enter to expand or collapse answer.Answer expanded
- Option D is correct because the sectors in the circle graph can be estimated as follows. The sector for blue has a central angle that is very close to a right angle, which is about 25% of the circle, and the sector for red is somewhat less than half the circle, perhaps about 45% of the circle. Thus, blue and red together constitute about 25% plus 45%, or 70%, of the data. It follows that yellow and green together constitute about 30% of 850, or 255 students. Among the options, 250 is closest to 255. Option A is incorrect because it is at least one order of magnitude less than the estimate given in option D. Option B is incorrect because it is at least one order of magnitude less than the estimate given in option D. Option C is incorrect because the estimate of 150 is about 18% of 850; therefore, if blue is about 25% of the data, then red could be greater than 50% of the data, which would contradict the graph.
29. The height of each student at Jefferson Middle School was measured and recorded. Joseph was told that his height was at the 60th percentile of the heights of the students. Which of the following must be true?
- The heights of 4 students are greater than Joseph's height.
- Joseph's height is 60 inches.
- The heights of at least 60 percent of the students are less than or equal to Joseph's height.
- If the height of the tallest student is 70 inches, then Joseph's height is left paren 0.6 right paren left paren 70 right paren equals 48 inches.
- Enter to expand or collapse answer.Answer expanded
- Option C is correct because a percentile is a measure used in statistics that indicates the value below which a given percent of observations in a group of observations fall. Joseph's height at the 60th percentile of the heights of students means that the heights of at least 60 percent of the students are less than or equal to Joseph's height. Option A is incorrect because the total number of students is not given. Option B is incorrect because none of the heights are given. Option D is incorrect because being at the 60th percentile of the heights measured does not mean that Joseph's height is 60 percent of the height of the tallest student.
List L: 4, 9, 4, 8, 9, 8, 11, 10, 9
30. List L is shown above. Let overline x be the mean, let m be the median, and let D be the mode of the numbers in list L. Which of the following is true?
- overline x equals m and m equals D
- overline x equals m and m is less than D
- overline x is less than m and m equals D
- overline x is less than m and m is less than D
- Enter to expand or collapse answer.Answer expanded
- Option C is correct. The mean of the numbers in the list is the sum of the numbers divided by the number of numbers in the list, overline x equals fraction 4 plus 9 plus 4 plus 8 plus 9 plus 8 plus 11 plus 10 plus 9 over 9 equals fraction 72 over 9 equals 8. To find the median, arrange the numbers in list L in increasing order: 4, 4, 8, 8, 9, 9, 9, 10, 11. There are 9 numbers in the list. The median is the number in the middle of the list, that is, the fifth number, m equals 9. The mode of the numbers in a list is the number in the list that appears the most often: in this case D equals 9. Thus, overline x is less than m and m equals D. Options A and B are incorrect because overline x does not equal m. Option D is incorrect because m equals D.
Competency 013—The teacher understands the theory of probability.
31. To form a committee, a principal will choose 3 students from a group of 5 seventh-grade students and 2 students from a group of 6 eighth-grade students. What is the total number of different committees the principal could select?
- 16
- 150
- 180
- 720
- Enter to expand or collapse answer.Answer expanded
- Option B is correct because the number of combinations of n objects taken k at a time is given by the formula n over k equals fraction n factorial over k factorial left paren n minus k right paren factorial. If the principal chooses 3 students from a group of 5 seventh-grade students and 2 students from a group of 6 eighth-grade students, the number of possible different committees is left paren 5 over 3 right paren left paren 6 over 2 right paren equals start fraction 5 factorial over 3 factorial 2 factorial end fraction start fraction 6 factorial over 2 factorial 4 factorial end fraction equals left paren start fraction 5 times 4 times 3 times 2 times 1 over left paren 3 times 2 times 1 right paren left paren 2 times 1 right paren end fraction right paren left paren start fraction 6 times 5 times 4 times 3 times 2 times 1 over left paren 2 times 1 right paren left paren 4 times 3 times 2 times 1 rigth paren end fraction right paren equals left paren 10 right paren left paren 15 right paren equals 150. Options A, C and D are incorrect because the calculations are not correct.
32. Six swimmers are competing in a 25-meter race. If there are no ties, how many different combinations are possible for a first-, second-, and third-place finish?
- 216
- 120
- 18
- 15
- Enter to expand or collapse answer.Answer expanded
- Option B is correct because it is possible for any of the 6 swimmers to finish first, which leaves 5 possible second-place finishers and 4 possible third-place finishers. Using the multiplication rule, there are 6 times 5 times 4 equals 120 possible combinations. Option A is incorrect because this is the result of 6 cubed, which does not take into consideration that the swimmer who finishes first cannot finish second or third, and the swimmer who finishes second cannot finish third. Option C is incorrect because this is the result of 6 times 3. Option D is incorrect because this is the result of 6 plus 5 plus 4.
There are two parent nodes representing events A and B. The diagram indicates that event A has a .6 probability of occurring, and event B has a .4 probability of occurring. Two more nodes representing events C and D extend from event A. According to the diagram, if event A occurs, the probabilities for events C and D to occur are .6 and .4, respectively.
33. Mr. Garcia showed his mathematics class the probability tree diagram shown above, where 0.6 and 0.4 represent the probability that an event will occur. Based on the diagram, what is the probability that event D will occur?
- 1.00
- 0.36
- 0.24
- 0.20
- Enter to expand or collapse answer.Answer expanded
- Option C is correct. Probability tree diagrams can be used to represent a series of independent events. Each node on the diagram represents an event and the probability that the event will occur is shown. The parent node represents a certain event and has probability 1. Each set of subsequent nodes represents an exclusive and exhaustive partition of the parent event. The probability associated with a node is the probability of that event occurring after the parent event occurs. For example, in the tree diagram shown, the probability that event A will occur is 0.6. The probability that the series of events leading to a particular node will occur is equal to the product of the probability that node will occur times the probabilities of the occurrence of the preceding events. In the diagram shown, the probability that event D will occur is the product of the probability that event A will occur times the probability that event D will occur, P left paren D right paren equals left paren 0.6 right paren left paren 0.4 right paren equals 0.24. Option A is incorrect because 1.00 is the sum of 0.6 and 0.4, while the probability that event D will occur is the product of 0.6 and 0.4. Option B is incorrect because 0.36 is the product of 0.6 and 0.6, which is the probability that event C will occur. Option D is incorrect because the probability that event D will occur is the product left paren 0.6 right paren left paren 0.4 right paren and not the difference, 0.6 minus 0.4.
34. A high school issues each new student a 7-character identifier. The first 3 characters are the first 3 letters in the student's last name, all capital letters from the 26-character English alphabet. The 3 letters are followed by 4 randomly generated integers from 0 to 9, inclusive. Repetition of letters and integers is allowed. How many unique identifiers can be generated?
- left paren 26 cubed right paren left paren 10 to the power of 4 right paren
- left paren 26 right paren left paren 25 right paren left paren 24 right paren left paren 10 to the power of 4 right paren
- left paren 26 right paren left paren 25 right paren left paren 24 right paren left paren 10 right paren left paren 9 right paren left paren 8 right paren left paren 7 right paren
- fraction left paren 26 factorial right paren left paren 10 factorial right paren over left paren 3 factorial right paren left paren 23 factorial right paren left paren 4 factorial right paren left paren 6 factorial right paren
- Enter to expand or collapse answer.Answer expanded
- Option A is correct. There are 26 possible letters that can be chosen for the first letter in the 7-character identifier. Since repetition is allowed, there are also 26 possible choices for the second and third letters. Then the number of possible letter combinations is 26 cubed. Similarly, since repetition is allowed for the integer characters, the number of possible combinations of the 4 integers in the identifier is 10 to the power of 4. The total number of unique identifiers is thus left paren 26 cubed right paren left paren 10 to the power of 4 right paren. Option B is incorrect because left paren 26 right paren left paren 25 right paren left paren 24 right paren is the number of possible 3-letter combinations if repetition is not allowed. Option C is incorrect because left paren 26 right paren left paren 25 right paren left paren 24 right paren left paren 10 right paren left paren 9 right paren left paren 8 right paren left paren 7 right paren is the number of 7-character identifiers if repetition is not allowed for either the letters or the integers. Option D is incorrect because fraction left paren 26 factorial right paren left paren 10 factorial right paren over left paren 3 factorial right paren left paren 23 factorial right paren left paren 4 factorial right paren left paren 6 factorial right paren is the number of combinations of 26 letters taken 3 at a time multiplied by the number of combinations of 10 integers taken 4 at a time.
Competency 014—The teacher understands the relationship among probability theory, sampling and statistical inference and how statistical inference is used in making and evaluating predictions.
Use the information below to answer the question that follows.
The table has two columns, labeled Time, T, in hours, and Number of Bacteria, in thousands. The horizontal T axis of the graph is labeled Time in hours, with values marked from 0 to 10 in increments of 2. The vertical axis is labeled Number of Bacteria in thousands. The data points on the graph correspond to the values in the table. I will now read the data values.
Time, 0. Number of Bacteria, 10,000.
Time, 1. Number of Bacteria, 18,000.
Time, 2. Number of Bacteria, 35,000.
Time, 3. Number of Bacteria, 85,000.
Time, 4. Number of Bacteria, 170,000.
Time, 5. Number of Bacteria, 300,000.
Time, 6. Number of Bacteria, 600,000.
Time, 7. Number of Bacteria, 1,300,000.
Time, 8. Number of Bacteria, 2,500,000.
35. Every hour, a scientist counted the number of bacteria growing in a certain medium. The scientist recorded the results in a table and produced the scatterplot shown above. If P of t is a mathematical model for the number of bacteria, in thousands, at time t hours, which of the following expressions is the best fit for P of t?
- P of t = 300t + 10
- P of t = 300t squared + 100t + 10
- P of t = 10 times 2 to the t
- P of t = 10 times the natural log of 2t + 1
- Enter to expand or collapse answer.Answer expanded
- Option C is correct. Based on the scatterplot, an exponential function is the best model for the data shown. Evaluation of P left paren t right paren equals 10 left paren 2 to the power of t right paren for values of t is greater than or equal to O shows that this function produces values close to the data recorded. Option A is incorrect because the data shown in the scatterplot are not linear. Option B is incorrect because a parabola is not the best fit for the data shown in the scatterplot. Option D is incorrect because a logarithmic function is not the best fit for the data shown.
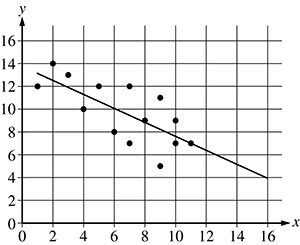
The x and y axes have values marked from 0 to 16 in increments of 2. There is a line drawn from an x value of 1 and a y value of 13 to an x value of 16 and a y value of 4. There are about a dozen data points scattered loosely around the line between x values of 1 and 11 and y values between 5 and 14.
36. The scatterplot shows the relationship between two sets of data, x and y. The line of best fit of the relationship between the two data sets is shown. Based on the line of best fit, which of the following is the best estimate of the value of y when the value of x is 14?
- 0
- 2
- 5
- 7
- Enter to expand or collapse answer.Answer expanded
- Option C is correct. Based on the graph of the line of best fit, we can determine that when the value of x is 14, then the value of y is between 4 and 6. Given the four answer choices, option C, 5, is the best answer. Options A, B, and D are incorrect because 5 is the best estimate of the value of y when x is 14.
37. In 2016 there were 324,582 licensed teachers in a certain state. The ages of the teachers were modeled with a normal distribution. The mean age was 43.5 years old, with a standard deviation of 8.2 years. Based on this distribution, which of the following is the best estimate of the number of licensed teachers in the state in 2016 with an age of 59.9 years old or greater?
- 8000 teachers
- 16,000 teachers
- 55,000 teachers
- 110,000 teachers
- Enter to expand or collapse answer.Answer expanded
- Option A is correct. The graph of a normal distribution is bell-shaped and symmetric about a vertical line through its center. The mean, median, and mode of a normal distribution are all equal and occur at the center of the distribution. About 68% of all data values of a normal distribution lie within 1 standard deviation of the mean, in both directions. About 95% of the data values lie within 2 standard deviations of the mean, in both directions. Thus, about 2.5% of the data values are greater than 2 standard deviations about the mean. The mean is given to be 43.5 years old with a standard deviation of 8.2 years, and 43.5 plus 2 left paren 8.2 right paren equals 59.9. Therefore, about 2.5% of the 324,582 licensed teachers in the state are 59.9 years old or older, and start fraction 2.5 over 100 end fraction left paren 324,582 right paren equals 8114 which is almost equal to 8000. Option B is incorrect because 16,000 licensed teachers is about 5% of the total number of teachers. Option C is incorrect because 55,000 licensed teachers is about 17% of the total. Option D is incorrect because 110,000 is about 34% of the total.
Domain V—Mathematical Processes and Perspectives
Competency 015—The teacher understands mathematical reasoning and problem solving.
Use the figure and the proof below to answer the question that follows.
The angles all appear to be different. A B is longer than B C, and A C is longer than A B.
Given: In triangle ABC shown, A B is greater than B C
Prove: angle A is not equal to angle C, that is the measure of angle A is not equal to the measure of angle C.
Proof by contradiction: Assume that angle A is congruent to angle C.
If angle A is congruent to angle C, then line A B is congruent to line A C by the blank. However, this theorem contradicts the given information that A B is greater than B C. Therefore, the assumption that angle A is congruent to angle C must be false, and so the measures of the angles cannot be equal and angle A is not equal to to angle C.
38. In the proof above, which of the following theorems correctly fills in the blank?
- corresponding angles theorem
- angle bisector theorem
- isosceles triangle theorem
- congruence of triangles with the side-side-side property
- Enter to expand or collapse answer.Answer expanded
- Option C is correct because the converse of the isosceles triangle theorem is the statement that if two angles of a triangle are congruent, then the sides opposite the two angles are congruent. Option A is incorrect because the corresponding angles theorem involves two parallel lines and a transversal. Option B is incorrect because the angle bisector theorem involves an angle that is bisected. Option D is incorrect because the side-side-side comparison is used to determine if two triangles are congruent.
Use the figure and the proof below to answer the question that follows.
In triangle A B C, the long leg, A B, is horizontal, and the short leg, B C is vertical. A line is drawn from vertex B to point D on the hypotenuse, forming a right angle with the hypotenuse and dividing A C into two segments. Segment C D is labeled p, and segment A D is labeled q. Triangle A B C is now divided into 2 right triangles, B C D and A B D. Side C B is labeled A and forms the hypotenuse of triangle B C D. Side A B is labeled b and forms the hypotenuse of triangle ABD. Beside the diagram is an equation, p + q = c.
| Statement | Reason |
|---|---|
| p over A = A over c, and q over b = b over c | 1. ? |
| p = A squared over c, and q = b squared over c | 2. Multiplication property of equality |
| c = p + q = A squared over c + b squared over c | 3. Substitution. |
| c squared = A squared + b squared | 4. Multiplication property of equalit |
39. A seventh-grade mathematics teacher presented the proof of the Pythagorean theorem shown above, with one missing reason for students to supply. What is the missing reason?
- Triangles CDB and BDA are similar.
- Apply the angle-side-angle theorem to triangle BDA.
- Apply the side-angle-side theorem to triangle CBA.
- Triangles CBA and CDB are similar, and triangles CBA and BDA are similar.
- Enter to expand or collapse answer.Answer expanded
- Option D is correct because the similarity of triangle CBA and CDB implies that the lengths of their corresponding sides have the same ratio, yielding p over a equals a over c. Similarly, the similarity of triangles CBA and BDA yields q over b equals b over c. Option A is incorrect because although it is true that triangles CDB and BDA are similar, c is not equal to any of the lengths of the sides of these triangles. Options B and C are incorrect because the angle-side-angle and side-angle-side theorems refer to the congruence of triangles.
Competency 016—The teacher understands mathematical connections within and outside of mathematics and how to communicate mathematical ideas and concepts.
40. A teacher would like to instruct students about semiregular tessellations of a plane. A semiregular tessellation of a plane uses more than one type of regular polygon. Also, every vertex in the tessellation has the same arrangement of polygons around it, where the sum of the angles around the vertex is 360 degrees. The teacher proposes a tessellation that uses three types of regular polygons: a 15-gon, a triangle, and a third type. What is the third type of regular polygon?
- A pentagon
- A hexagon
- An octagon
- A decagon
- Enter to expand or collapse answer.Answer expanded
- Option D is correct because the measure of an interior angle of a regular 15-gon is left paren 15 minus 2 right paren left paren 180 degrees right paren over 15, or 156 degrees. When 156 degrees is added to 60 degrees, the measure of an interior angle of an equilateral triangle, the result is 216 degrees. Then 360 degrees minus 216 degrees equals 144 degrees. The equation left paren n minus 2 right paren left paren 180 degrees right paren over n equals 144 degrees can be used to determine that n = 10, and therefore, the third type of polygon is a decagon. Option A is incorrect because an interior angle of a regular pentagon measures 108 degrees, not 144 degrees. Option B is incorrect because an interior angle of a regular hexagon measures 120 degrees, not 144 degrees. Option C is incorrect because an interior angle of a regular octagon measures 135 degrees, not 144 degrees.
Use the student work below to answer the question that follows.

Student Work.
Using the figure below, determine if the following statement is true or false, and explain your reasoning.
Statement: m angle C is less than m angle F.
There are diagrams of 2 right triangles side by side. In triangle A B C, the long leg, A C, is horizontal and dimensioned as 4. The short leg, A B, is vertical and dimensioned as 3. The hypotenuse, B C, is dimensioned as 5. In triangle D E F, the long leg, D F, is horizontal and dimensioned as 12. The short leg, D E, is vertical and dimensioned as 9. The hypotenuse, E F, is dimensioned as 15.
True or False. True is circled. Why? Because triangle D E F is bigger and line D E is longer than line A B.
41. Which of the following is the most appropriate way for a mathematics teacher to respond to the student work shown?
- The student's work is correct.
- The student's calculations are correct, but the teacher should ask the student to calculate the measure of each angle.
- The student's work is incorrect because the angle measures are not given and cannot be determined from the information provided.
- The student's work is incorrect because the triangles are similar; therefore, m angle C = m angle F.
- Enter to expand or collapse answer.Answer expanded
- Option D is correct because the two triangles are similar since the corresponding sides have the same ratio; therefore, the corresponding angles must be congruent. Options A and B are incorrect because angle C and angle F are, in fact, congruent, so their measures are equal. Option C is incorrect because although the student's work is not correct and the angle measures are not given, the angle measures can, in fact, be determined from the information given using inverse trigonometric functions; for example, m angle C = arcsin left paren 3 over 5 right paren.
42. Rachel and Peter deposited 25,000 dollars into a new savings account with an annual interest rate of 3.5 percent, compounded semiannually. If they do not make any withdrawals from the account or make any other deposits to the account, which of the following is closest to the balance in the account after three years?
- 26,335.60 dollars
- 27,625.00 dollars
- 27,742.56 dollars
- 30,731.38 dollars
- Enter to expand or collapse answer.Answer expanded
- Option C is correct. If a principal of P dollars is invested at an annual interest rate of r percent compounded n times per year, and no further withdrawals or deposits are made to the account, then the future value A of the account balance after t years is given by the formula A equals P left paren 1 plus fraction r over 100n right paren to the power of nt. In this problem, P is 25,000 dollars; n is 2 (semiannually means two times per year); r is 3.5 percent, which becomes 0.035 in the formula; and t is 3 years. When those values are substituted into the formula shown, the future value A of the account balance will be A = 25,000 dollars left paren 1 plus fraction 0.035 over 2 right paren to the power of (2)(3) = $27,742.56. Option A is incorrect because the number of compounded periods is left paren 3 right paren left paren 2 right paren equals 6, not just 3. Option B is incorrect because the interest is compounded; therefore, the interest rate for three years is not the simple interest of left paren 3 right paren left paren 0.035 right paren equals 0.105. Option D is incorrect because $30,731 = $25,000(1 + 0.35)630,731 dollars equal 25,000 dollars left paren 1 plus 0.35 right paren to the power of 6, i.e., the interest is compounded semiannually, not annually.
43. In 2016 Mr. Schuppan paid an annual property tax of 1500 dollars. In 2017 Mr. Schuppan paid an annual property tax of 1650 dollars. What was the percent increase of Mr. Schuppan's property tax from 2016 to 2017?
- 8.03%
- 9.09%
- 10.0%
- 15.0%
- Enter to expand or collapse answer.Answer expanded
- Option C is correct. The percent increase of Mr. Schuppan's property tax from 2016 to 2017 is start fraction 1650 minus 1500 over 1500 end fraction times 100% equals start fraction 150 over 1500 end fraction times 100% equals 10%. Options A and D are incorrect because they are obtained by computational errors. Option B is incorrect because 9.09% is the percent change with respect to the 2017 tax instead of the 2016 tax.
Domain VI—Mathematical Learning, Instruction and Assessment
Competency 017—The teacher understands how children learn and develop mathematical skills, procedures and concepts.
Use the example below to answer the question that follows.
start fraction 2x to the power of 4 minus 3x cubed plus x squared minus 4x plus 5 over x minus 1 end fraction
44. A teacher is preparing a unit on polynomial long division and would like to use the problem shown above as an example. Before discussing the example, of the following, which concept is best for the teacher to review?
- Multiplying two rational expressions
- Vertical asymptotes
- The additive property of equality
- The division algorithm for real numbers
- Enter to expand or collapse answer.Answer expanded
- Option D is correct because the division algorithm for real numbers should be familiar to the students. The same algorithm is used in polynomial long division. Option A is incorrect because the multiplication of rational expressions is not needed in polynomial long division. Option B is incorrect because the unit is about polynomial long division. A vertical asymptote may be a feature of the graph of a rational function in the xy-plane and should be discussed in a unit on graphing. Option C is incorrect because the additive property of equality is useful for solving equations for a variable but is not necessary in polynomial long division.
start fraction 36x cubed y negative squared z to the power of 4 over 18x squared y negative cubed z to the power of 6 end fraction
45. A teacher is preparing a unit about simplifying algebraic expressions and would like to use the expression shown above as an example. Before discussing the example, which of the following concepts is best for the teacher to review?
- The zero-product property of multiplication
- Extraneous solutions
- The laws of exponents
- The properties of multiplication of real numbers
- Enter to expand or collapse answer.Answer expanded
- Option C is correct because simplifying the expression requires application of the laws of exponents. Option A is incorrect because the expression is not set equal to zero; the student is not asked to solve for a variable. Option B is incorrect because the student is not asked to solve for a variable, and thus no extraneous solutions will be produced. Option D is incorrect because the laws of exponents are the primary group of operations used to simplify the expression.
Competency 018—The teacher understands how to plan, organize and implement instruction using knowledge of students, subject matter and statewide curriculum (Texas Essential Knowledge and Skills [TEKS]) to teach all students to use mathematics.
46. Marcus is renting a bicycle. The rental requires a down payment of 15 dollars plus 6 dollars for each hour the bicycle is rented. If C is the total charge and t is the number of hours that Marcus rented the bicycle, which of the following equations represents the relationship between the amount of time he rented the bicycle and the total cost?
- C equals 1 sixth t plus 15
- C equals 6t plus 15
- C equals 15t plus 6
- C equals 15 left paren t minus 1 right paren plus 6
- Enter to expand or collapse answer.Answer expanded
- Option B is correct because in order to compute the total cost for t hours, the price per hour must be multiplied by the number of hours and added to the down payment, resulting in C equals 6t plus 15. Option A is incorrect because the cost per hour in this model would be 1 sixth of a dollar rather than 6 dollars. Options C and D are incorrect because the cost per hour in this model would be 15 dollars rather than 6 dollars.
47. A mathematics teacher assigns students in a sixth-grade class to keep a mathematics diary. Every day, the students are asked to record when and how they use mathematics in their daily lives. At the end of each week, the students each write a short report on their use of mathematics, and the teacher reviews their diaries. Which of the following is the teacher demonstrating with this activity?
- An understanding of a variety of questioning strategies to encourage mathematical discourse and to help students analyze, evaluate, and communicate their mathematical thinking
- An understanding of the use of inductive reasoning to make conjectures and deductive methods to evaluate the validity of conjectures
- An understanding of the purpose, characteristics, and uses of summative assessments
- An understanding of how technological tools and manipulatives can be used appropriately to assist students in developing, comprehending, and applying mathematical concepts
- Enter to expand or collapse answer.Answer expanded
- Option A is correct because the primary purpose of this activity is to engage the students in mathematical discourse and develop their communication skills. Option B is incorrect because inductive reasoning may be used but is not the primary focus. Option C is incorrect because this activity is not part of a summative assessment. Option D is incorrect because technology and manipulatives are not necessarily used in this activity.
48. Let f of x equals left paren x minus 100 right paren left paren x minus 125 right paren left paren x minus 150 right paren left paren x minus 175 right paren. A student wants to use a graphing calculator to find the points in the xy-plane where the graph of f crosses the x-axis. Which of the following bounds on x can be used in a viewing window so that the calculator displays all the points where the graph of f crosses the x-axis?
- negative 391,000 is less than or equal to x which is less than or equal to 75
- negative 200 is less than or equal to x which is less than or equal to negative 75
- negative 100 is less than or equal to x which is less than or equal to 99
- 75 is less than or equal to x which is less than or equal to 200
- Enter to expand or collapse answer.Answer expanded
- Option D is correct because the zeros of the function are 100, 125, 150, and 175. If the window on the graphing calculator is set to 75 is less than or equal to x which is less than or equal to 200, then all the x-intercepts of the graph in the xy-plane will be displayed. Option A is incorrect because this window does not include the zeros of the function. The minimum value of the function is negative 390,625, so negative 391,000 is an appropriate value for the lower bound of the y values. Options B and C are incorrect because these ranges do not include the zeros of the function on the x-axis.
Competency 019—The teacher understands assessment and uses a variety of formal and informal assessment techniques to monitor and guide mathematics instruction and to evaluate student progress.
49. A mathematics teacher finished a unit on adding fractions and gave a formative assessment. While grading the assessment, the teacher found that more than half of the students were making the error start fraction a over b end fraction plus start fraction c over d end fraction equals start fraction a plus c over b plus d end fraction. Which of the following is the best way for the teacher to address this error?
- Reviewing fraction addition and giving another formative assessment with questions designed to determine common errors among the students
- Moving to the next section in the text and including questions on fraction addition on the summative review at the end of the semester
- Asking the students to perform a search of newspapers and Web sites and document how fractions are used in news stories
- Moving to the next section in the text and assigning extra-credit homework on fraction addition
- Enter to expand or collapse answer.Answer expanded
- Option A is correct because the formative assessment showed that students need additional instruction and practice in adding fractions. Formative assessments can be designed to determine common errors and misconceptions. Options B and D are incorrect because students should be able to add fractions correctly before learning new material. Option C is incorrect because, while newspaper and Web site searches are interesting and helpful, they do not address the issue of fraction addition.
50. A mathematics teacher finishes a unit on multiplying expressions with exponents and gives a formative assessment. While grading the assessment, the teacher finds that more than half of the students made the error left paren 2 to the power of 4 right paren left paren 2 to the power of 5 right paren equals 2 to the power of 20. Which of the following is the best description of the error?
- The students multiplied the exponents instead of adding the exponents.
- The students should have expanded 2 to the power of 4 equals 16 and 2 to the power of 5 equals 32 then multiplied the numbers instead of using the properties of exponents.
- The students should not have omitted the multiplication sign between the two numbers in parentheses.
- The students should have expanded the answer, 2 to the power of 20, to an integer.
- Enter to expand or collapse answer.Answer expanded
- Option A is correct because left paren 2 to the power of 4 right paren left paren 2 to the power of 5 right paren equals 2 to the power of 4 plus 5 equals 2 to the power of 9. Options B, C, and D are incorrect because left paren a to the power of b right paren left paren a to the power of c right paren equals a to the power of b plus c not a to the power of bc.