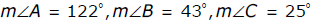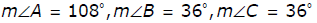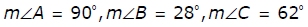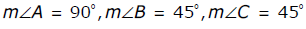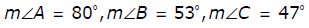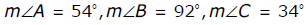Skip to main content

Preparation Manual

Print this page

Section 5: Sample Selected-Response Questions
Core Subjects 4–8 Subject Exam II—Mathematics Subtest (807)

Expand All Answers | Collapse All Answers

This section presents some sample exam questions for you to review as part of your preparation for the Subject Exam. To demonstrate how each competency may be assessed, sample questions are accompanied by the competency that they measure. While studying, you may wish to read the competency before and after you consider each sample question. Please note that the competency statements do not appear on the actual exam.

For each sample exam question, there is a correct answer and a rationale for each answer option. The sample questions are included to illustrate the formats and types of questions you will see on the Subject Exam; however, your performance on the sample questions should not be viewed as a predictor of your performance on the actual exam.

The following reference materials will be available to you during the exam:

Subject Exam II Sample Questions

Competency 001—The teacher understands the structure of number systems, the development of a sense of quantity and the relationship between quantity and symbolic representations.

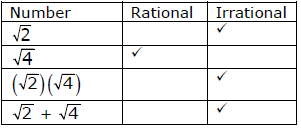
1. Indicate whether the following numbers are rational or irrational by checking the appropriate boxes.

Number Rational Irrational
the square root of 2 Blank. Blank.
the square root of 4 Blank. Blank.
the square root of 2 times the square root of 4 Blank. Blank.
the square root of 2 plus the square root of 4 Blank. Blank.
Enter to expand or collapse answer.Answer expanded
The checked options are correct because the square root of 2 is irrational, the square root of 4 equals 2" is rational, the square root of 2 times the square root of 4 equals 2 times the square root of 2 is irrational and the square root of 2 plus the square root of 4 is irrational.
Table with three columns and 5 rows representing the number and whether it is rational or irrational. The options that are not checked are incorrect. The first column is labeled number, the second column is labeled rational, and the third column is labeled irrational. The second row begins with the square root of 2 which has rational unchecked and irrational checked. The third row begins with the square root of 4 which has rational checked and irrational unchecked. The fourth row begins with the square root of 2 multiplied by the square root of 4 which has rational unchecked and irrational checked. The fifth row begins with the square root of 2 plus the square root of 4 which has rational unchecked and irrational checked. The options that are not checked are incorrect.

Competency 003—The teacher understands ideas of number theory and uses numbers to model and solve problems within and outside of mathematics.

Use the figure below to answer the question that follows.

diagram of routes available between the flower shop, the hotel, the hospital, and the restaurant.

The routes from the flower shop be used to reach the hotel by Jefferson Street, Jackson Street, and Taft Street. The routes from the hotel can be used to reach the hospital by Canal Street and Main Street. The routes from the hospital can be used to reach the restaurant by 38th street, Durango Avenue, and Union Street. The routes from the restaurant can be used to get back to the flower shop by Barton Street and Soledad Street.

2. Jennifer is a delivery person for a flower shop. Using the map above, how many different routes are there for Jennifer to choose from if she travels from the flower shop to the hotel, then to the hospital, then to the restaurant, and then back to the flower shop?

  1. 6
  2. 10
  3. 18
  4. 36
Enter to expand or collapse answer.Answer expanded
Option D is correct because there are three ways to travel from the flower shop to the hotel, two ways to travel from the hotel to the hospital, three ways to travel from the hospital to the restaurant, and two ways to travel from the restaurant back to the flower shop. So by the multiplication rule of counting, 3 × 2 × 3 × 2 = 36 routes. Options A, B and C are incorrect because the numbers 3, 2, 3 and 2 are all multiplied to the get the number of routes. These numbers are not added together nor are they a subset of the numbers multiplied together.

Competency 004—The teacher understands and uses mathematical reasoning to identify, extend and analyze patterns and understands the relationships among variables, expressions, equations, inequalities, relations and functions.

Use the table below to answer the question that follows.

x y
6 19
9 28
12 37
15 46

3. Which of the following lines in the xy-plane includes the points in the table shown?

  1. y equals x plus 3.
  2. y equals x plus 13.
  3. "y equals 3 x plus 1.
  4. y equals 3 x plus 13.
Enter to expand or collapse answer.Answer expanded
Option C is correct because the slope of the line described by the information in the table can be found to be 28 minus 19 over 9 minus 6 equals 9 over 3 equals 3. . The slope-intercept form of the line is y equals 3 x plus b. , where b is the y-intercept. The value of b can be found by substituting one of the (x, y) values from the table as follows.
19 = 3(6) + b19 equals 3 left paren 6 right paren plus b.
19 = 18 + b19 equals 18 plus b.
1 = b1 equals b.
Substituting the value of b in the equation gives y equals 3 x plus 1. Option A is incorrect because if x = 6 then y = 9, which is not in the table. Option B is incorrect because if x = 19 then y = 32, which is not in the table. Option D is incorrect because if x = 6 then y = 31, which is not in the table.

4. Jeb pays $18 per night for a campsite every time he takes a trip to Palmetto State Park. Last year he camped 4 nights in Palmetto State Park each month. This year he purchased a state park pass for $70. With his park pass, he receives 50% off 24 nights of camping for the entire year. Let x be the number of nights he will get to camp this year for the amount he spent last year. Which of the following equations could be used to find x?

  1. 0.5 times 18 x plus 70 equals 864.
  2. 18 x minus 0.5 times 24 x plus 70 equals 864.
  3. 18 x plus 0.5 multiplied by 18 multiplied by 24 plus 70 equals 864.
  4. 18 x minus 0.5 multiplied by 18 multiplied by 24 plus 70 equals 864.
Enter to expand or collapse answer.Answer expanded
Option D is correct because last year Jeb paid $18 a night for 4 nights a month for all 12 months, which totals $864. He wants to spend the same amount this year and go camping for x nights at the same rate of $18 a night. He also pays an additional $70 for the 24 discounted nights. So his cost is 18 x plus 70 dollars minus his discount of left paren 0.5 right paren left paren 24 right paren left paren 18 right paren" dollars. Option A is incorrect because the discount is only for 24 nights of camping, not for the charge per night. Option B is incorrect because the discount is only for 24 nights, and is not dependent on the value of x. Option C is incorrect because the application of a discount is obtained by subtraction, not addition.

Competency 006—The teacher understands and uses nonlinear functions and relations to model and solve problems.

Use the functions below to answer the question that follows.

g of x equals 3 left paren x minus 2 right paren squared plus 5.
h of x equals 3 left paren x minus 2 right paren squared plus 9.

5. How is the graph of h in the xy-plane related to the graph of g?

  1. The graph of h is the graph of g shifted 4 units to the right.
  2. The graph of h is the graph of g shifted 4 units to the left.
  3. The graph of h is the graph of g shifted 4 units upward.
  4. The graph of h is the graph of g shifted 4 units downward.
Enter to expand or collapse answer.Answer expanded
Option C is correct because functions are shifted upward or downward when constants are added to or subtracted from the original function, respectively. In this case h of x equals g of x plus 4. so the graph shifts 4 units upward. Options A, B and D are incorrect because h of x equals g of x plus 4. and the shift of the graph of g is vertically up, not horizontally left or right or vertically down.

Competency 008—The teacher understands measurement as a process.

Use the figure below to answer the question that follows.

A right triangle with points labels as A, B, and C.

C is located at the right angle. The adjacent leg has a length of 2 miles and the angle from C is labeled A. From a the hypotenuse to the opposite side is not labeled. The acute angle is labeled B. From point B to C there is a length of 2 miles.

6. Town C is 2 miles east of Town A and 2 miles south of Town B, as in the figure above. Which of the following is the best estimate of the shortest distance from Town A to Town B?

  1. 2 miles
  2. 2.8 miles
  3. 3.4 miles
  4. 4 miles
Enter to expand or collapse answer.Answer expanded
Option B is correct because Towns A, B and C create a right triangle with legs of length 2 and 2. The length of the hypotenuse, x, is the distance between A and B, x. By the Pythagorean theorem,
x squared equals 2 squared plus 2 squared.
x squared equals 8
x equals the square root of 8 which is approximately equal to 2.8.
Another way to obtain the solution is to note that the triangle shown is a 45°–45°–90° triangle. The rule of isosceles right triangles is that the hypotenuse has a length of one of the legs times a factor of square root of 2, then 2 multiplied by the square root of 2 which is approximately equal to 2.8 Options A, C and D are incorrect because the shortest distance between two points in the plane is given by the Pythagorean theorem, the distance of 2 miles is too short, and the distances of 3.4 and 4 miles are longer that the shortest distance between Towns A and B.

Competency 009—The teacher understands the geometric relationships and axiomatic structure of Euclidian geometry.

7. Let

  1. 2 x minus 3 y equals 5
  2. 3 x plus 2 y equals 5
  3. 3 x minus 2 y equals 0
  4. 2 x plus 3 y equals 15
Enter to expand or collapse answer.Answer expanded
Option B is correct because the slope of line liquid is 2 over 3 and the slope of a line perpendicular to line liquid is the opposite of the reciprocal, i.e., . The slope-intercept form of a line perpendicular to line liquid will be y equals negative 3 over 2 x plus b where b is any real number. The only equation, when solved for y, that fits this form is 3 x plus 2 y equals 5 Option A is incorrect because the line 2 x minus 3 y equals 5 has slope 2/32 over 3. and is parallel to liquid. Option C is incorrect because the line 3 x minus 2 y equals 0. has slope 3 over 2. and is not perpendicular to liquid. Option D is incorrect because the line 2 x plus 3 y equals 15. has slope negative 2 over 3. and is not perpendicular to liquid..

8. Triangle ABC is an obtuse triangle. Which of the following are possible measurements of angles in the triangle ABC ?

Select all that apply.

  1. the measure of angle a is 122 degrees, the measure of angle b is 43 degrees, the measure of angle C is 25 degrees
  2. the measure of angle a is 108 degrees, the measure of angle b is 36 degrees, the measure of angle C is 36 degrees
  3. the measure of angle a is 90 degrees, the measure of angle b is 28 degrees, the measure of angle C is 62 degrees
  4. the measure of angle a is 90 degrees, the measure of angle b is 45 degrees, the measure of angle C is 45 degrees
  5. the measure of angle a is 80 degrees, the measure of angle b is 53 degrees, the measure of angle C is 47 degrees
  6. the measure of angle a is 54 degrees, the measure of angle b is 92 degrees, the measure of angle C is 34 degrees
Enter to expand or collapse answer.Answer expanded
Options B and F are correct because obtuse triangles contain one angle whose measure is greater than 90 degrees. Options C, D and E are incorrect because no angles have measures greater than 90 degrees. Option A is incorrect because the sum of the angles is 190 degrees instead of 180 degrees.

Competency 010—The teacher analyzes the properties of two- and three-dimensional figures.

Use the figure below to answer the question that follows.

an diagram of room shape created with two smaller shapes which is a square labeled Room A on top of an octogon labeled Room B.

9. Michael is designing a new home for a customer. The floor of Room B is in the shape of a regular hexagon and will have a perimeter of 72 feet. The floor of Room A is in the shape of a square and will be sharing a wall with Room B as shown. How many square feet of carpet will Michael need to cover the floor of Room A ?

  1. 48 square feet
  2. 120 square feet
  3. 144 square feet
  4. 864 square feet
Enter to expand or collapse answer.Answer expanded
Option C is correct because Room B is a regular hexagon, which means each of the six sides are congruent, and the perimeter is 72 feet. This means that each wall of Room B is 72 over 6 equals 12. feet. Because Room A is a square and shares a wall with Room B, all of the walls in Room A are also 12 feet. Then 12 squared equals 144. square feet of carpet will be needed to cover Room A’s floor. Option A is incorrect because 48 feet is the perimeter, not the area of Room A. Option B is incorrect because 120 square feet is less than the correct area. Option D is incorrect because 864 square feet results from multiplying the two perimeters together 72 by 12.

Competency 012—The teacher understands how to use graphical and numerical techniques to explore data, characterize patterns and describe departures from patterns.

Use the table below to answer the question that follows.
College Graduate Annual Salary
A 36,000 dollars
B 35,250 dollars
C 71,555 dollars
D 34,750 dollars
E 35,575 dollars

10. The table shows five college graduates and the annual salaries they earned during their first year in the workforce. Based on the data given in the table, which of the following statements is true?

  1. The mean is less than the range of the data.
  2. The mean is less than the median of the data.
  3. The range is less than the mean of the data.
  4. The range is less than the median of the data.
Enter to expand or collapse answer.Answer expanded
Option C is correct because the mean is 42,626 dollars, the median is $35,575 and the range is $36,805, so the range is less than the mean. Option A is incorrect because the mean is greater than the range. Option B is incorrect because the mean is greater than the median. Option D is incorrect because the range is greater than the median.

Competency 013—The teacher understands the theory of probability.

11. Each face of a number cube is numbered 1, 2, 3, 4, 5 or 6. When the cube is tossed, each number is equally likely to appear face up. The number cube is tossed twice, and the numbers that land face up are recorded. What is the probability that the sum of the two recorded numbers is a prime number?

  1. 1 over 2 or one half.
  2. 8 over 21.
  3. 5 over 36.
  4. 15 over 36.
Enter to expand or collapse answer.Answer expanded
Option D is correct because there are five prime numbers between 1 and 12: 2, 3, 5, 7 and 11. There are 36 total outcomes of the two tosses, and in 15 of the tosses the sum of the two recorded numbers will be a prime number.

1 + 1 = 2 2 + 3 = 5 4 + 3 = 7
1 + 2 = 3 2 + 5 = 7 5 + 2 = 7
1 + 4 = 5 3 + 2 = 5 5 + 6 = 11
1 + 6 = 7 3 + 4 = 7 6 + 1 = 7
2 + 1 = 3 4 + 1 = 5 6 + 5 = 11
Option A is incorrect because 1 over 2 or one half. is the probability that the sum of the two recorded numbers is odd, and not every odd number is prime. Option B is incorrect because the denominator should be the number of total possible outcomes, which is 36. A denominator of 21 represents the number of outcomes if the order of outcomes is not accounted for as different outcomes (e.g., if a roll of a 4 and then a 3, or a 3 and then a 4 is counted as one outcome instead of two). Eight is the amount of times the sum is prime if only these 21 outcomes are considered. Option C is incorrect because even though there are five prime numbers between 1 and 12, there is more than one way to generate a prime as the sum of the two recorded numbers.

Competency 016—The teacher understands mathematical connections within and outside of mathematics and how to communicate mathematical ideas and concepts.

12. Students in a mathematics class are using graphing calculators to find the maximum and minimum values of the graph of f of x equals 2 sin 3 x. on the domain .left bracket 0 comma 2 pi right bracket. One student reports to the teacher that the calculator is only displaying a straight line. The teacher verifies that the equation has been entered correctly and that the graphing window is correct. Which of the following is the best suggestion for the student in order to see the periodic behavior of the graph of the function over the domain?

  1. Use the Zoom-In function
  2. Check if the calculator is in degree mode or in radian mode
  3. Check if the calculator is in function mode or in polar mode
  4. Check if a StatPlot is on
Enter to expand or collapse answer.Answer expanded
Option B is correct because viewing the function f of x equals 2 sin 3 x. in degrees mode would stretch one period of the function to 120 degrees. Restricting the domain to .left bracket 0 comma 2 pi right bracket. limits the graphing window to display a part of the graph that resembles a linear function. If the mode is changed to radians, the period of the function will be 2 pi over 3, and the window will display 3 full periods of the curve. Option A is incorrect because zooming in on the graph will not allow the student to see the required features of the graph. Option C is incorrect because the teacher has already checked that the equation has been entered correctly in function mode. Option D is incorrect because a StatPlot being on might result in an error when trying to graph simultaneously with a function, but this will not change the view of the function being graphed.

13. Tammy is applying for a loan to purchase her first home. Her annual salary is 58,356 dollars but the loan officer is asking for her monthly gross income and her monthly net income. If 15 percent of her total income is paid in taxes each month, what are her monthly gross income and her monthly net income? (Gross income is income before taxes. Net income is income after taxes).

  1. Her monthly gross income is 729 dollars and 45 cents, and her monthly net income is .4863 dollars
  2. Her monthly gross income is 4863 dollars, and her monthly net income is 728 dollars and 45 cents..
  3. Her monthly gross income is 4863 dollars, and her monthly net income is 4133 dollars and 55 cents..
  4. Her monthly gross income is 4133 dollars and 55 cents, and her monthly net income is 4863 dollars.
Enter to expand or collapse answer.Answer expanded
Option C is correct because Tammy’s monthly gross income equals her annual salary divided by 12, which is 4863 dollars. Because her taxes are 15 percent of her income, her monthly net income equals the remaining 85 percent, which is 4133 dollars and 55 cents.. Option A is incorrect because 729 dollars and 45 cents is the amount of Tammy’s taxes each month and 4863 dollars is her monthly gross income. Option B is incorrect because 729 dollars and 45 cents is the amount of Tammy’s taxes each month, not her monthly net income. Option D is incorrect because the values for the monthly gross and monthly net incomes are switched.

Competency 018—The teacher understands how to plan, organize and implement instruction using knowledge of students, subject matter and statewide curriculum (Texas Essential Knowledge and Skills [TEKS]) to teach all students to use mathematics.

14. A teacher provides students with a square sheet of paper for an in-class activity. The teacher asks the students to fold the paper in half, unfold the paper, and color one of the sections created by the fold, and determine what fraction of the paper they colored. The students then refold the paper on the same fold and fold it in half once more. Before unfolding the paper, the teacher asks the class how many sections the paper now has, and how many of those sections will be colored. Which skill is the teacher introducing to the students with the activity?

  1. Modeling fractional quantities greater than 1 using concrete objects and pictorial models
  2. Estimating measurements, including circumference, and evaluating reasonableness of results
  3. Using concrete objects and pictorial models to generate equivalent fractions
  4. Using models to relate decimals to fractions that name tenths, hundredths and thousandths
Enter to expand or collapse answer.Answer expanded
Option C is correct because when the original coloring of the paper is done, 1 over 2 or 1 half. of the paper is colored. Then after the next fold, 2 over 4 or 2 fourths. of the paper is colored, but no additional coloring was added or removed. This demonstrates that .1 half equals 2 fourths. Option A is incorrect because in the activity, the subdivisions of one unit are created, not quantities greater than one. Option B is incorrect because the activity models fractions not measurements or circumference. Option D is incorrect because the fractions modeled are halves and fourths, not tenths, hundredths or thousandths.
Return to Navigation